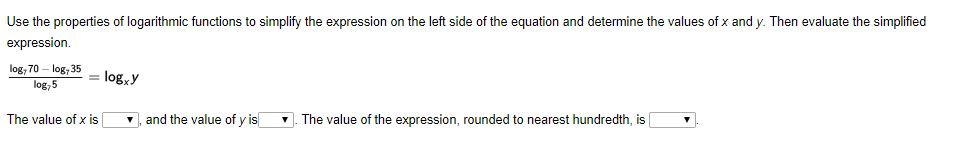Question

logarithmic functions to simplify the expression

Answer 1

Basic rules:
Product: \[\large\rm \log_b(\color{red}{x }\cdot \color{blue}{y}) = \log_b\color{red}{ x} + \log_b \color{blue}{y}\]
Quotient: \[\large\rm \frac{ \log_b\color{red}{ x} }{ \log_b \color{blue}{y} }= log_b\color{red}{ x} - log_b\color{blue}{ y}\]

Answer 2

\[\frac{ \log_7 \color{Red}{70} - \log_7\color{blue}{{35}}}{ \log_7 5}\]

apply the quotient rule for top part

Answer 3

Oh ok thanks

Answer 4

{\displaystyle \log _{b}\!{\frac {x}{y}}=\log _{b}x-\log _{b}y}

@Nnesha pardon but i know this in this way

Answer 5

log_b x - log_b y = log_b (x/y)

Answer 6

yes. Thanks. typo
Quotient: \[\large\rm \log_b \frac{\color{red}{ x} }{ \color{blue}{y} }= log_b\color{red}{ x} - log_b\color{blue}{ y}\]
**

Answer 7

@Jbaena1 do you undestand the differens ?

Answer 8

on numerator there are

log_7 70 -log_7 35 = log_7 (70/35) = log_7 2

Answer 9

Ew. Logs.