Question

How to write the equation of a parabola knowing the focus and its directrix.

Answer 1

What we want to be doing:

'A parabola is defined as the set of all points that are the same distance away from a point (the focus) and a line (the directrix).'

Suppose you have a point (x,y) on the parabola. The distance between that point and the focus is equal to the distance between that point and the directrix.
Afterwards, we want to set them equal to each other to find the equation of the parabola.

For example lets say that our focus is (2, -2) and the directrix is at x=-4.
We first need to find the individual distances between the focus and point (x,y) AND the point (x,y) and the directrix.

So using the distance formula, we have the equation
\[\sqrt{(x-2)^2+(y+2)^2}\]

This is the equation of the distance between the focus and the point.

Now we have to find the distances between the point (x,y) and the directrix (x=-4)

Since the directrix is an x-value. We can ignore the y-value for now.
This is why:
\[\sqrt{x-(-4)+(y-y)^2}\] which equals \[\sqrt{(x+4)^2}\]

Now we have to equate the distances to derive the equation of the parabola.
\[\sqrt{(x-2)^2+(y+2)^2}=\sqrt{(x+4)^2}\]

(Square both sides)
\[(x-2)^2+(y+2)^2=(x+4)^2\]
Expand:
\[x^2-4x+4+(y+2)^2=x^2+8x+16\]
Solve for x:
\[(y+2)^2=12x+12\]
\[\sqrt{(y+2)^2}-12=12x\]
\[(\sqrt{(y+2)^2})/12-1\]
Now you know how to write the equation of a parabola knowing the focus and its directrix.

Answer 2

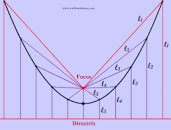
The directrix is the line in which all points in a plane are an equal distance away from and the focus is the point.

Answer 3

So like
Red lines are the same distance.

Answer 4

This leads to another important fact (unrelated but nevertheless important) which is that the focus and the directrix are the same distance apart from the vertex

Answer 5

k

Answer 6

If you have any questions you can ask me.

Answer 7

kk I will