Question

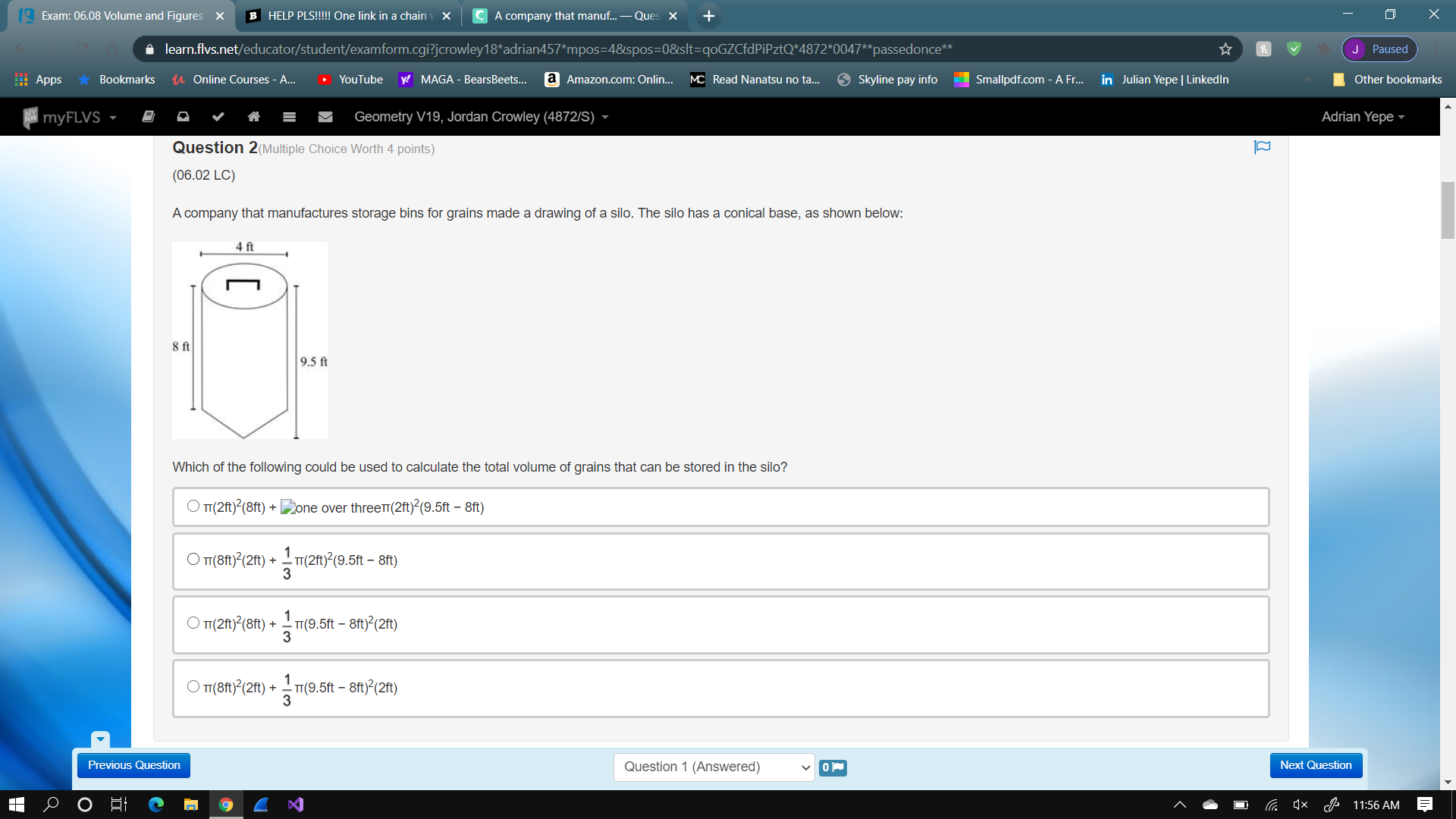
A company that manufactures storage bins for grains made a drawing of a silo. The silo has a conical base, as shown below:

The figure shows a silo shaped as a closed cylinder with a conical end. The diameter of the silo is 4 ft, the length of the cylindrical part is 8 ft, and the entire length of the silo is 9.5 ft.

Which of the following could be used to calculate the total volume of grains that can be stored in the silo?

π(2ft)2(8ft) + one over threeπ(2ft)2(9.5ft − 8ft)
π(8ft)2(2ft) + one over threeπ(2ft)2(9.5ft − 8ft)
π(2ft)2(8ft) + one over threeπ(9.5ft − 8ft)2(2ft)
π(8ft)2(2ft) + one over threeπ(9.5ft − 8ft)2(2ft)

Answer 1

This is what it looks like

Answer 2

pls help @MrMudd183

Answer 3

ok, so the first thing you need to know is the formula. do you know what that would be?

Answer 4

thats the part im confused about, since the silo is in the shape of a cylinider but also has a cone-shaped end, I'm not certain what formula to use

Answer 5

here's what i would to. i would make that one shape into two seperate shapes. so i would seperate the cone from the cylinider

Answer 6

\(\color{#0cbb34}{\text{Originally Posted by}}\) @MrMudd183
here's what i would to. i would make that one shape into two seperate shapes. so i would seperate the cone from the cylinider
\(\color{#0cbb34}{\text{End of Quote}}\)
do*

Answer 7

I see, that makes sense, but where exactly would you separate the two figures?

Answer 8

i would seperate it where i drew the blue line

Answer 9

so that way you have two seperate shapes. then you would find the volume of one and then use some of that info to get the volume for the other shape

Answer 10

Got it, thank you!

Answer 11

you're welcome