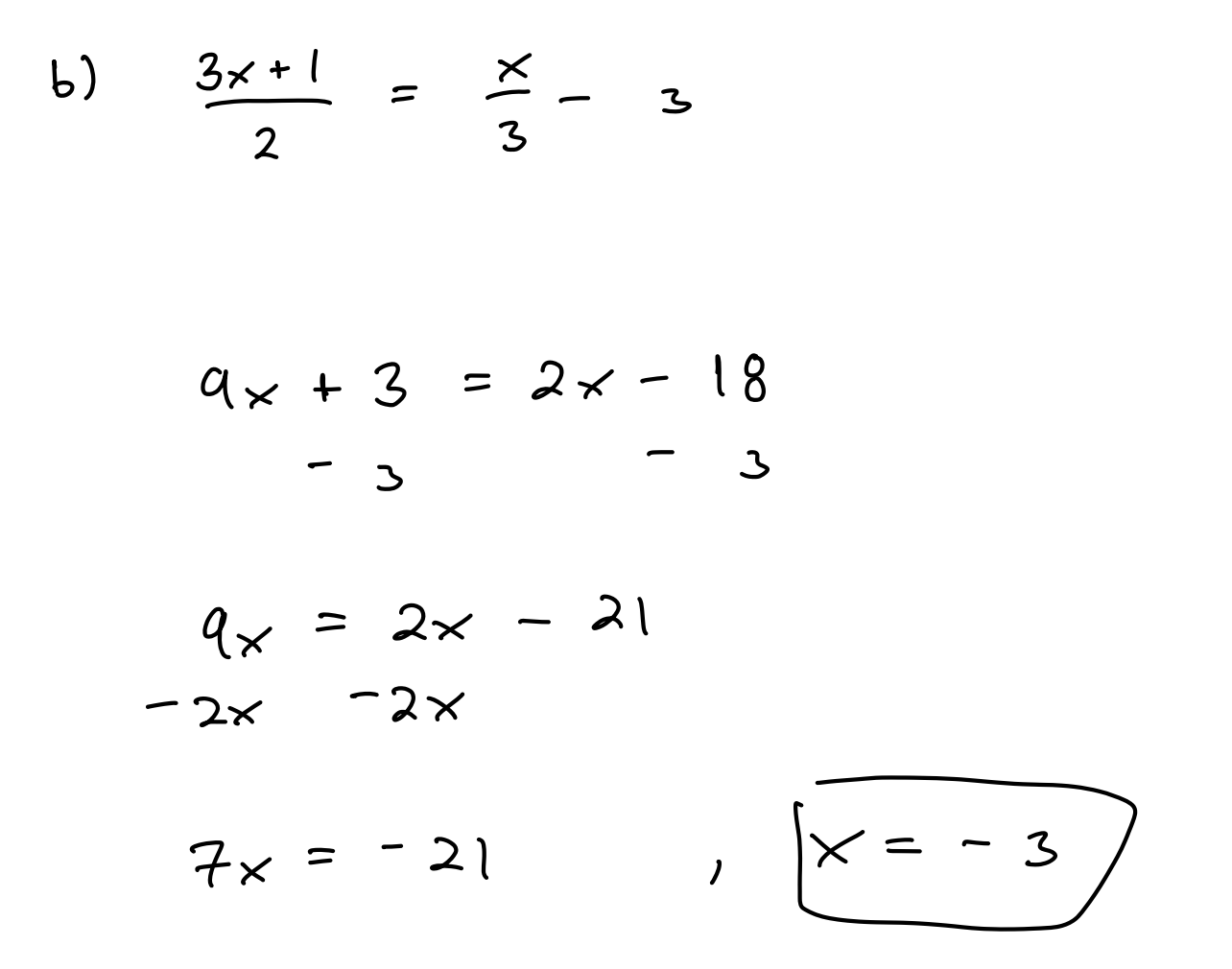can someone pls explain to me the steps of this problem? where did the 9x and 2x come from?
they multiplied both sides by 6 to get rid of the 2 and 3 denominators
wouldnt that make it 18x+6=6x-18?
notice the denominator of 2 on (3x + 1)/2 multiplying by 2 gets rid of the denominator multiplying by 3 turns it into 9x + 3 multiplying by 6 simply combines these two steps
if you're having trouble understanding the arithmetic: start from the beginning, multiply both sides by 2, then multiply both sides by 3
ok when i multiply both sides by 2 i get 6x+2=2x-6 then multiply both sides by 3, i get 18x+6=6x-18 am i multiplying something wrong?
(3x + 1) / 2 when you multiply by 2, the 2 in the denominator disappears, but the numerator does not change. (3x + 1) / 2 multiplied by 2 is simply 3x + 1
oh, so for the right side, why would it multiply out to 2x? do we ignore the denominator on that side too?
(x/3) * 6 = 2x if you want to think about it like this: (x/3) * 3 = x then x * 2 = 2x
apologies if i'm making this complicated, so after multiplying both sides by 2, i get: 3x+1=2x/3 - 6, then i multiply each side by 3 to get: 9x+3=2x-18 ^^ when multiplying by a fraction, i leave the denominator alone and just focus on the fraction?
just focus on the numerator* sorry
a/b * b = a when you're multiplying by the denominator, the denominator cancels out and you're left with the numerator only
ah ok thank you, that makes a lot more sense. sorry for being overcomplicated lol
my brain sometimes needs an explanation to understand arithmetic :p
Join our real-time social learning platform and learn together with your friends!