Question

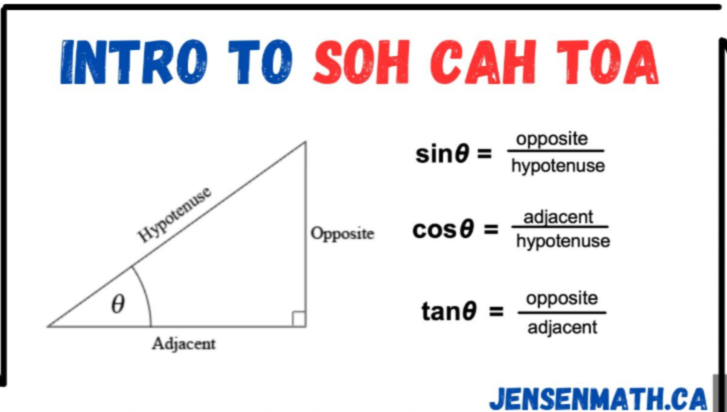
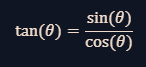What is the difference bewtween Sin, Cos, and Tan? What are they for? (Triganometry)

Answer 1

Imagine you have a right triangle with one of the non-right angles labeled θ. The triangle has three sides:

Opposite: The side directly across from the angle θ.

Adjacent: The side that forms the angle θ along with the hypotenuse.

Hypotenuse: The longest side (across the right angle).

Using these sides, the primary trigonometric ratios are defined as follows:

Key Differences
Definition in Terms of Sides:

Sine compares the length of the side opposite θ with the hypotenuse.

Cosine compares the length of the side adjacent to θ with the hypotenuse.

Tangent compares the length of the side opposite θ with the adjacent side. Notice that tangent can also be expressed as the ratio of sine to cosine:
Range and Behavior:

Sine and Cosine are both bound between -1 and 1, meaning their values never exceed this range regardless of the angle.

Tangent, however, can take on any real value. This is because as the angle approaches 90° (or π/2 radians), the cosine approaches 0, making the tan function blow up to infinity (or negative infinity in the other quadrant).

Unit Circle Perspective: In addition to right triangles, these functions are defined on the unit circle:

Sine (sin θ) is the y-coordinate of the point on the unit circle at an angle θ from the positive x-axis.

Cosine (cos θ) is the x-coordinate of that same point.

Tangent (tan θ) represents the slope of the line that connects the origin to that point (i.e., the ratio of the y-coordinate to the x-coordinate).

Applications and Contexts:

Sine might be used when you’re analyzing vertical forces, waves, or oscillatory motions.

Cosine is key in contexts that involve horizontal relationships, such as calculating distances in navigation.

Tangent is often helpful in finding the angle of elevation or slope, as it directly compares the change in height to the horizontal distance.

Diving Deeper
Think of these functions as different lenses through which you view the geometry of a triangle. They highlight different ratios, and depending on what you know about a triangle (one side, one angle, etc.), one might be more useful than the others. This is why in many applications—whether it's physics, engineering, or computer graphics—choosing the right function can simplify problem-solving.

Would you be interested in exploring how these functions extend into more complex topics like the unit circle, periodic functions, or even their role in Fourier analysis?



Hope this helps!

Answer 2

img. one

Answer 3

img. 2

Answer 4

omg, its trig!! (srry its smthing i geek out over) okay simple explanation (srry but i cant really understand the probably-ai-generated-response and me being me, i just wanna yap about it either way)

heres how i think of it:
cosine is like the x and sine is like the y in a xy axis kinda thing. tangent is y/x equation, so thats why you always gotta remember: tangent = sine over cosine. rise over run, those kinda things.

but thats for if a triangle happens to be on a graph, which later comes to use along with unit circles

- for the soh cah toa (gotta remember the saying! veryyy important) it means:
sine = opposite / hypotenuse (like a divided by sign lol)
cosine = adjacent / hypotenuse
tangent = opposite over adjecent

in every scenario where triangle is on the graph
- sine is always opposite to the theta symbole (yk, the 0 looking thing with a horizontal line through it)
- cosine is always the x axis itself. the theta, it's always at the center-ish to the origin as possible, and btw the triangle always touch the x axis so u now know how to put it on the graph cuz sine and cosine can be negative, depending where that triangle might be at in the graph (if yall guys are doing that)

since im not exactly sure which exact part of sine cosine and tangent ur asking, imma keep on going (sorry! its my favorite subject)

the sines and cosines are also the coordinate points on the unit circle. and again, cosine being the x point and sine being the y. and unit circles typically get a radias of one, which makes life a wholeeee lot easier. so if want the coordinate point of a point directly on top of the unit circle, it'd be (1,0) becase yk, thats the point of it in a normal graph. and so on..

i gotta do hw now tho but do tell me exactly what part u wanna know about :D ITS TRIG! i love trig. srry for the long yap tho

Answer 5

lol you love triganometry!

Answer 6

For SOH CAH TOA, an easier term to remember is "suck a toe", sounds odd but it works! (:

Answer 7

"Suck a toe" Thats crazy...

Answer 8

I am so confused

Answer 9

I have no idea...