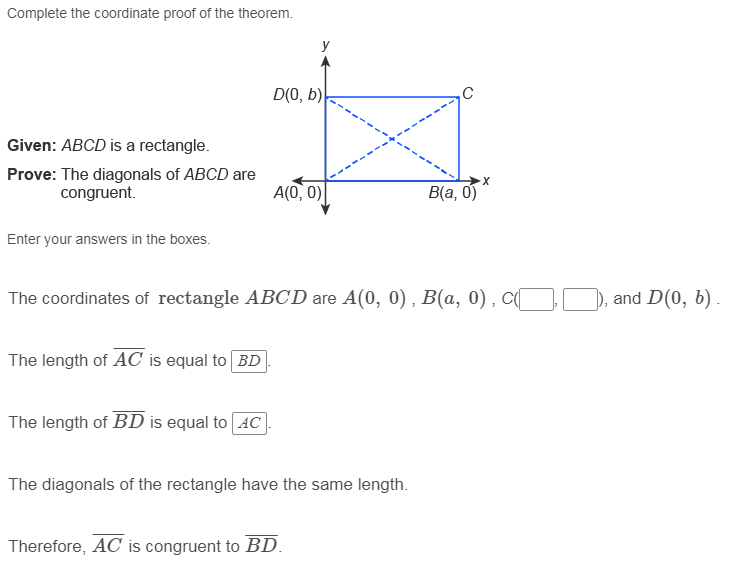
May someone please explain how do I solve this?
@Vocaloid
|dw:1510699424411:dw|Since B is located at (a,0), it means the bottom side of our rectangle has length a. Similarly, since d is located at (0,b), the left and right sides of our rectangle have length b.
|dw:1510699572655:dw|Use your Pythagorean Theorem to find the length of this diagonal. You've learned about this formula, yes? :o a^2 + b^2 = c^2
For our problem here, let's just call the hypotenuse AC. It satisfies this equation: a^2 + b^2 = (AC)^2 To solve for AC, the length of the diagonal, take square root. \[\large\rm \sqrt{a^2+b^2}=AC\]
|dw:1510699802161:dw|You can do the same for the other triangle, b^2 + a^2 = (BD)^2 \[\large\rm \sqrt{b^2+a^2}=BD\]
And coordinate C is located (a to the right) and (b up), C: (a, b)
Confusing? What do you think? :O
it is a little confusing, but i think i may understand
Nope I do not understand this, @Zepdrix do you think there is any possible way you could explain it simpler?
if you look at where C is positioned it has the same x-coordinate as B and the same y-coordinate as D
so point C is (x-coordinate of B,y-coordinate of D) --> replace these with the appropriate values/variables
Join our real-time social learning platform and learn together with your friends!