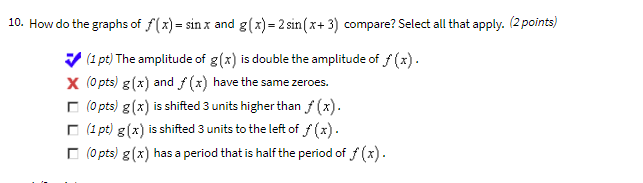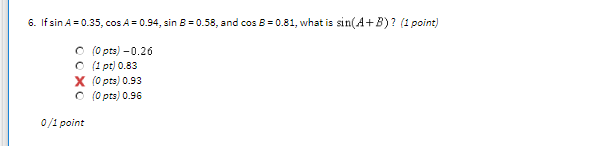kaylak:

doing corrections for math 6 questions please explain why my answer is wrong and why the other is correct @hero

1 month ago
kaylak:

1 attachment
1 month ago
Hero:

Okay, let's take a look. Go ahead and post the problems.

1 month ago
Hero:

\(f_{1}(x) = \sin(x)\) \(f_{2}(x) = 2\sin(x + 3)\) This one is pretty clear. The general form for trigonometric functions is \(f(x) = A\sin(Bx + C) + D\) where A represents the Amplitude. And clearly in the 2nd function, the amplitude is DOUBLE that of the 1st function.

1 month ago
Hero:

Because for \(f_{1}(x)\) \(A = 1\) and for \(f_{2}(x)\) \(A = 2\)

1 month ago
kaylak:

1 attachment
1 month ago
Hero:

For this one, all it is asking is to input the point (x,y) = (0,3) into each equation and check to see if both sides agree.

1 month ago
kaylak:

1 attachment
1 month ago
kaylak:

Idk this was like 4 months ago.. I'm done with course just trying to boost gpa.

1 month ago
Hero:

If I were you, I would have graphed each of the functions. But really, you were not going to be able to answer the question correctly unless you are thoroughly familiar with general forms of trig functions.

1 month ago
Hero:

Because even though they say the length from top to bottom is 5, the amplitude would only be half that.

1 month ago
Hero:

Knowing that would have enabled you to eliminate 3 of the answer choices right off the bat.

1 month ago
kaylak:

why is the answer for 15 exactly right and why is 24 correct want to get credit back

1 month ago
Hero:

Inputting (0,3) to y =sin(2x) + 3 yields: 3 = sin(2(0)) + 3 3 = sin(0) + 3 3 = 0 + 3 3 = 3 Inputting (0,3) to y = tan(x) + 3 yields: 3 = tan(0) + 3 3 = 0 + 3 3 = 3

1 month ago
Hero:

Your answer to 24 is here: All you had to do was graph it. The cycle completes every two seconds and the distance from top to bottom is 5: https://www.desmos.com/calculator/hriwr6pu9q

1 month ago
Hero:

@kaylak

1 month ago
kaylak:

1 attachment
1 month ago
kaylak:

last one

1 attachment
1 month ago
Hero:

You would use the sum-difference formula for sine to find the answer to number 6. And you would use the dot product formula to find the answer to number 5. Sorry I have to go for now. I'll be back later.

1 month ago
Click Here to Signup. You must be signed in to reply.
Similar Questions: