i need some answers checked
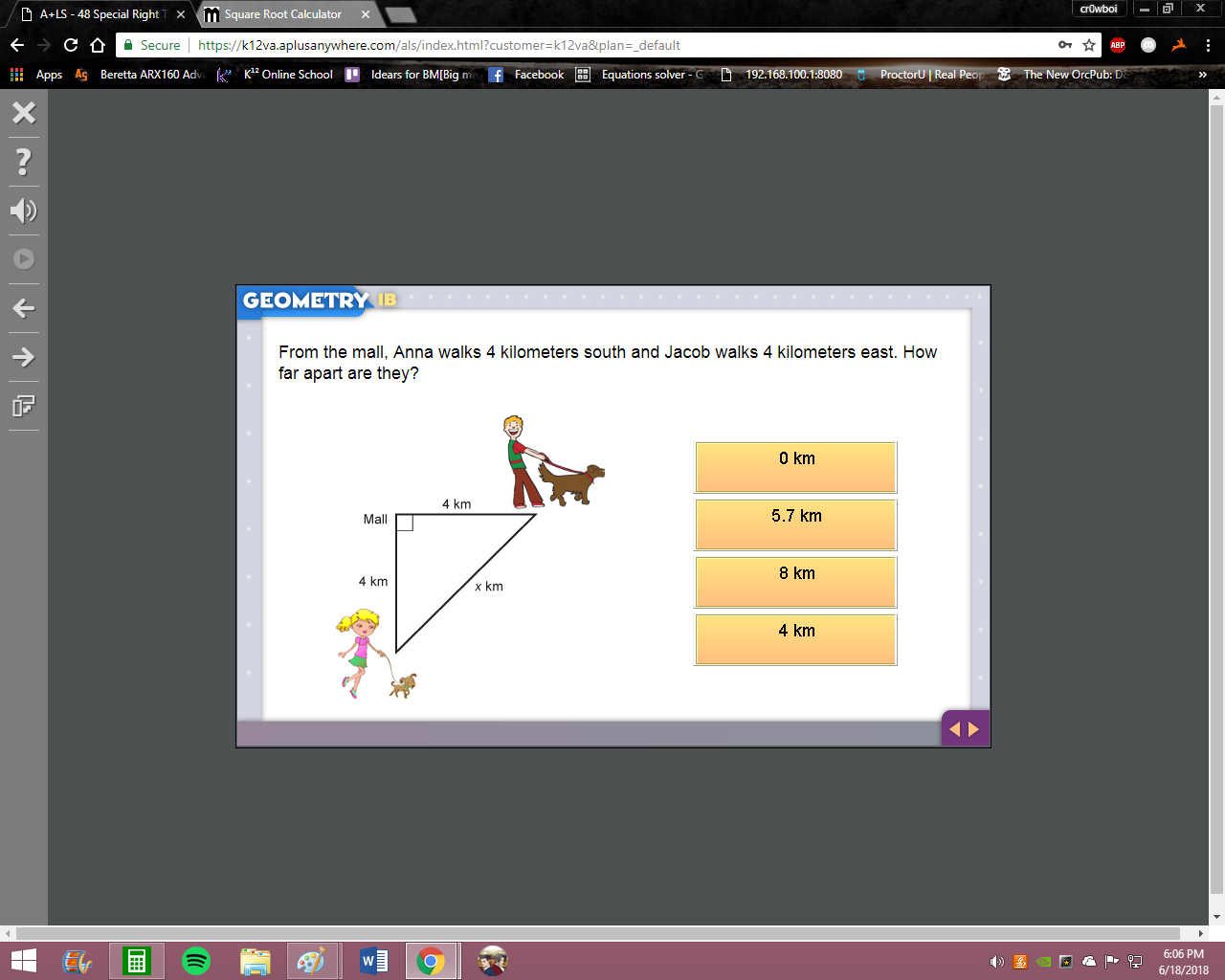
@Vocaloid my choice was the top right one
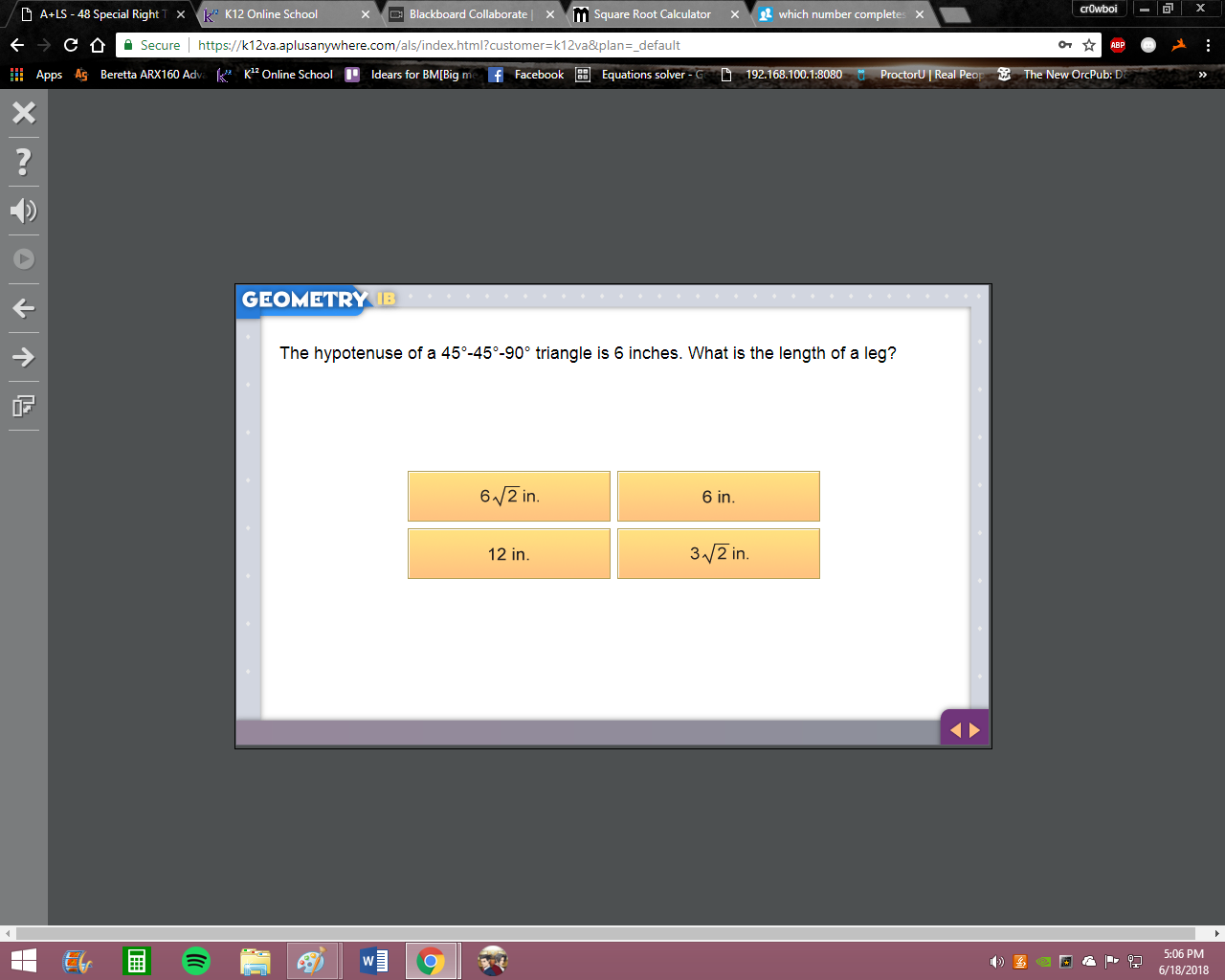
The leg and hypotenuse cannot both be 6. Remember what we said earlier: the leg of a 45-45-90 triangle is the hypotenuse divided by sqrt(2)
so it was the top left one?
Hypotenuse ~divided~ by sqrt(2) not multiplied.
so the bottom right one, as 3 is a multiple of 6?
Yes 6/sqrt(2) = 3sqrt(2)
i got A on this one
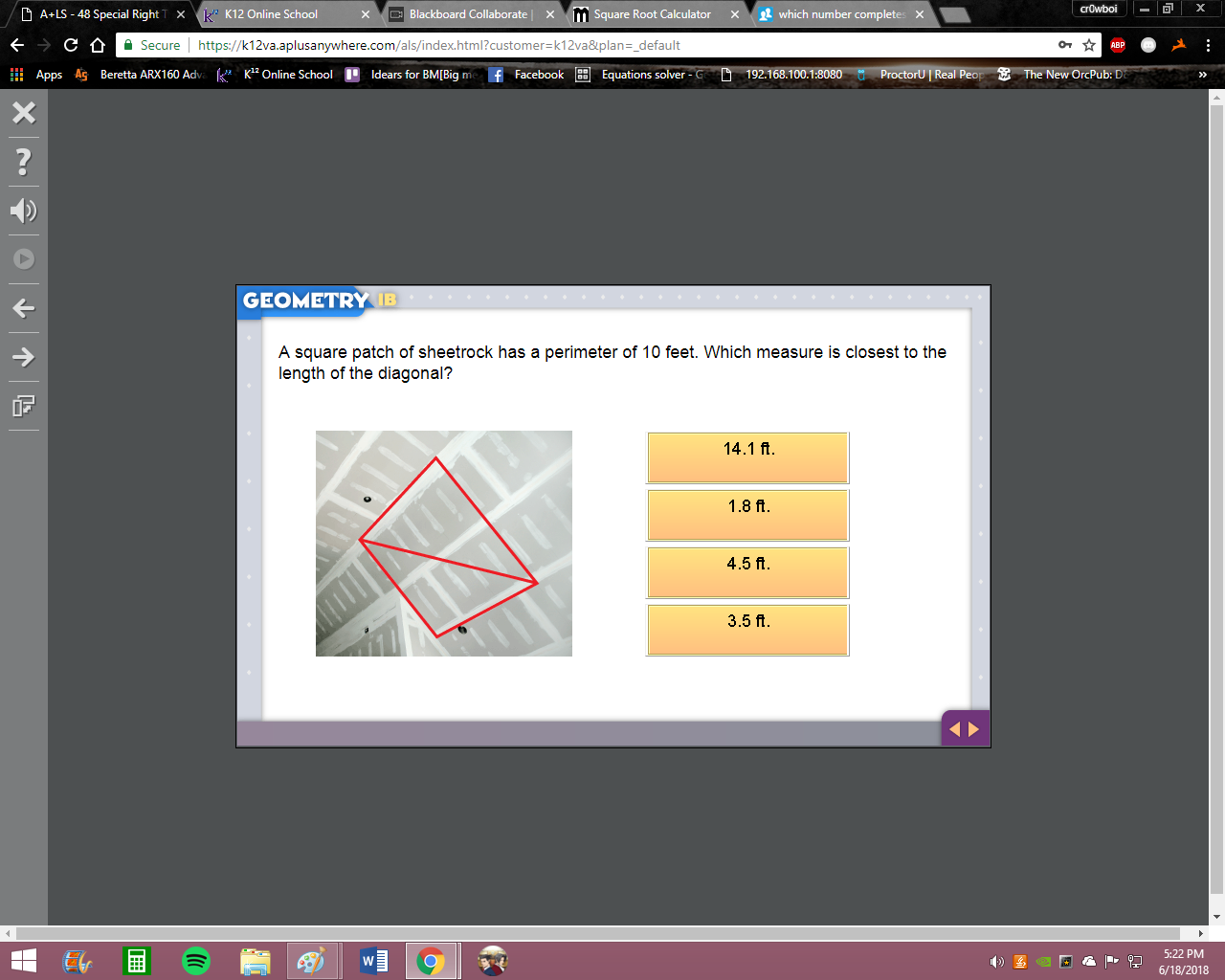
Nope First calculate the side length of the square using perimeter = 4s Then multiply by sqrt(2) because hypotenuse = leg * sqrt(2)
If the perimeter of a square is 10, then side length =?
Perimeter = 4* side length Solve for side length
so if the perimeter is 4, wouldnt that make it 1.8?
The perimeter is not 4 Please re-read the original problem
oh, right...
A square has four equal sides right? So the side length = perimeter/4
10/4=2.5
Good now multiply that by sqrt(2)
6.25
Check your calculations again Remember order of operations. Take the square root of 2 first and then multiply by 6
*multiply by 2.5 not 6
24?
hang on, i might've did it wrong again
Press the square root button, then 2 Press the enter button Then multiply by 2.5
so 4, x 2.5 = 10
Square root is not the same thing as squaring So the square root of 2 is not 4
Try this 2^(0.5) * 2.5
3.53
Good 3.5 is the only solution close enough so that's our answer
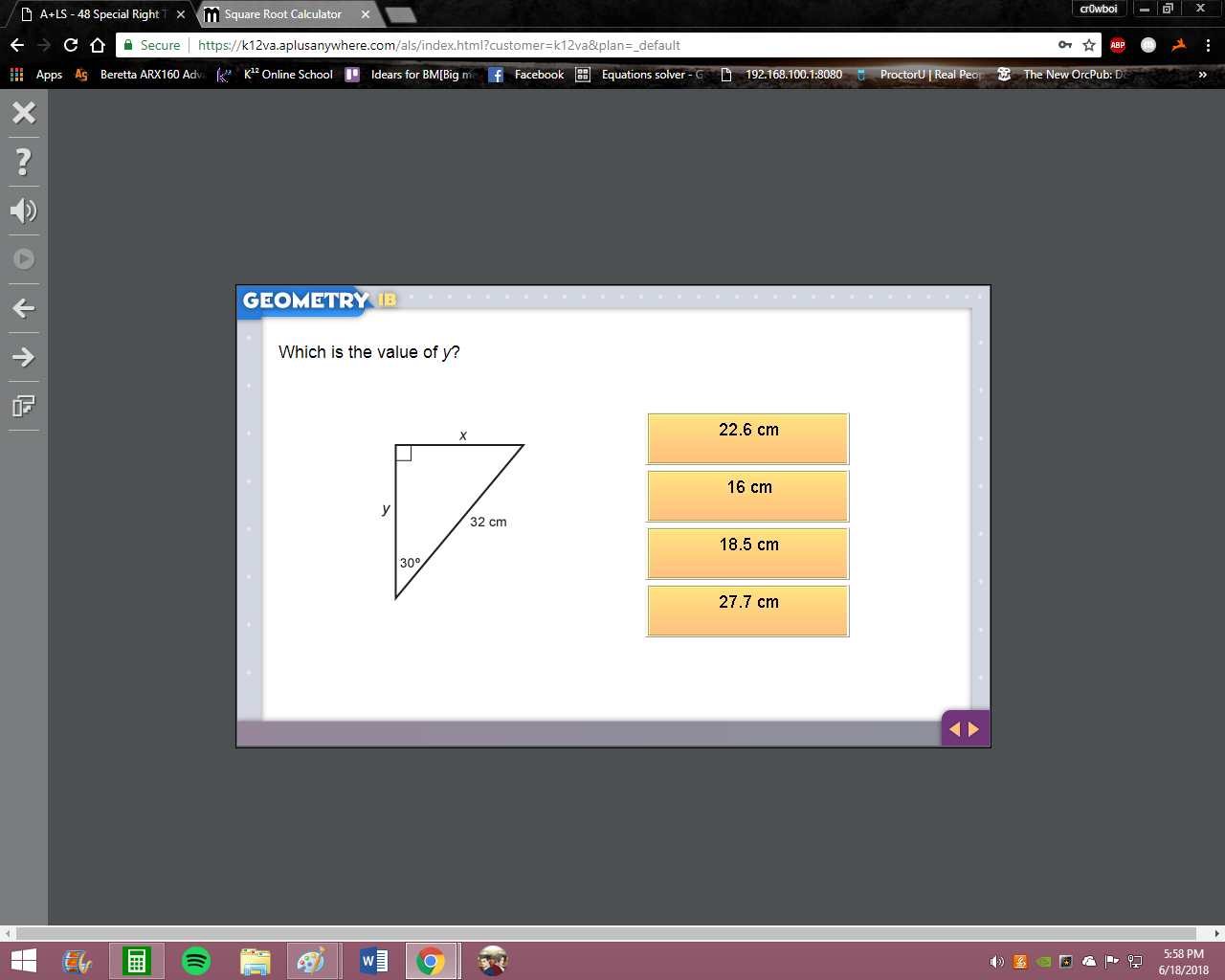
what i got on this, was 16.
Hm not quite, 16 would be the value of x not y To get y you just need to multiply 16 by sqrt(3) since y is the side across the 60 degree side
so D?
Good
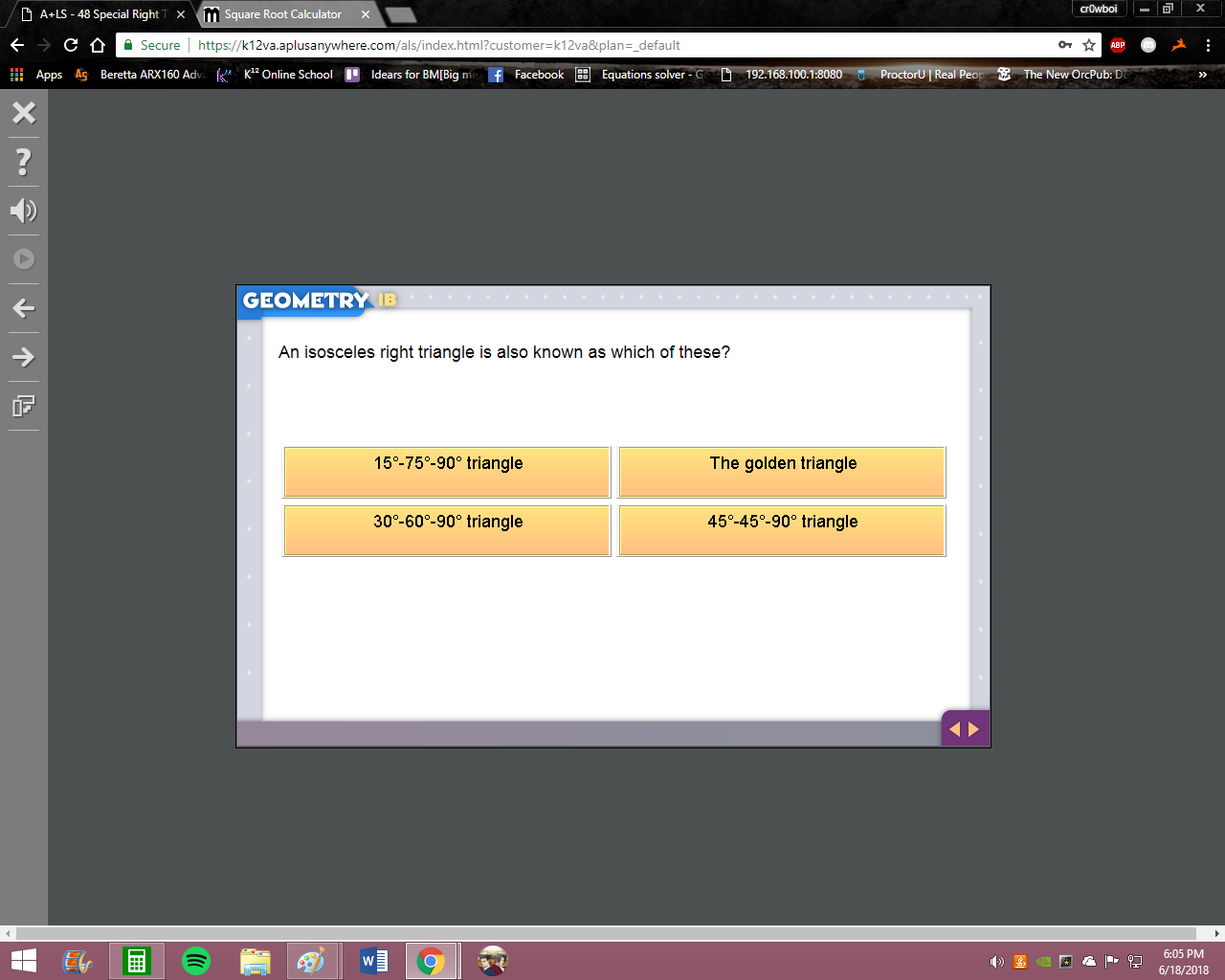
i chose the last one, as an isosceles is suppose to have two congruent sides, right?
Good
i chose C for this one
Hm not quite, 8 would be for a 30-60-90 triangle For a 45-45-90 triangle hypotenuse = leg * sqrt(2) =?
8?
or at least, 16?
The leg is 4 right? So sqrt(2) * 4 =?
5.6
so b
Good
false
Good
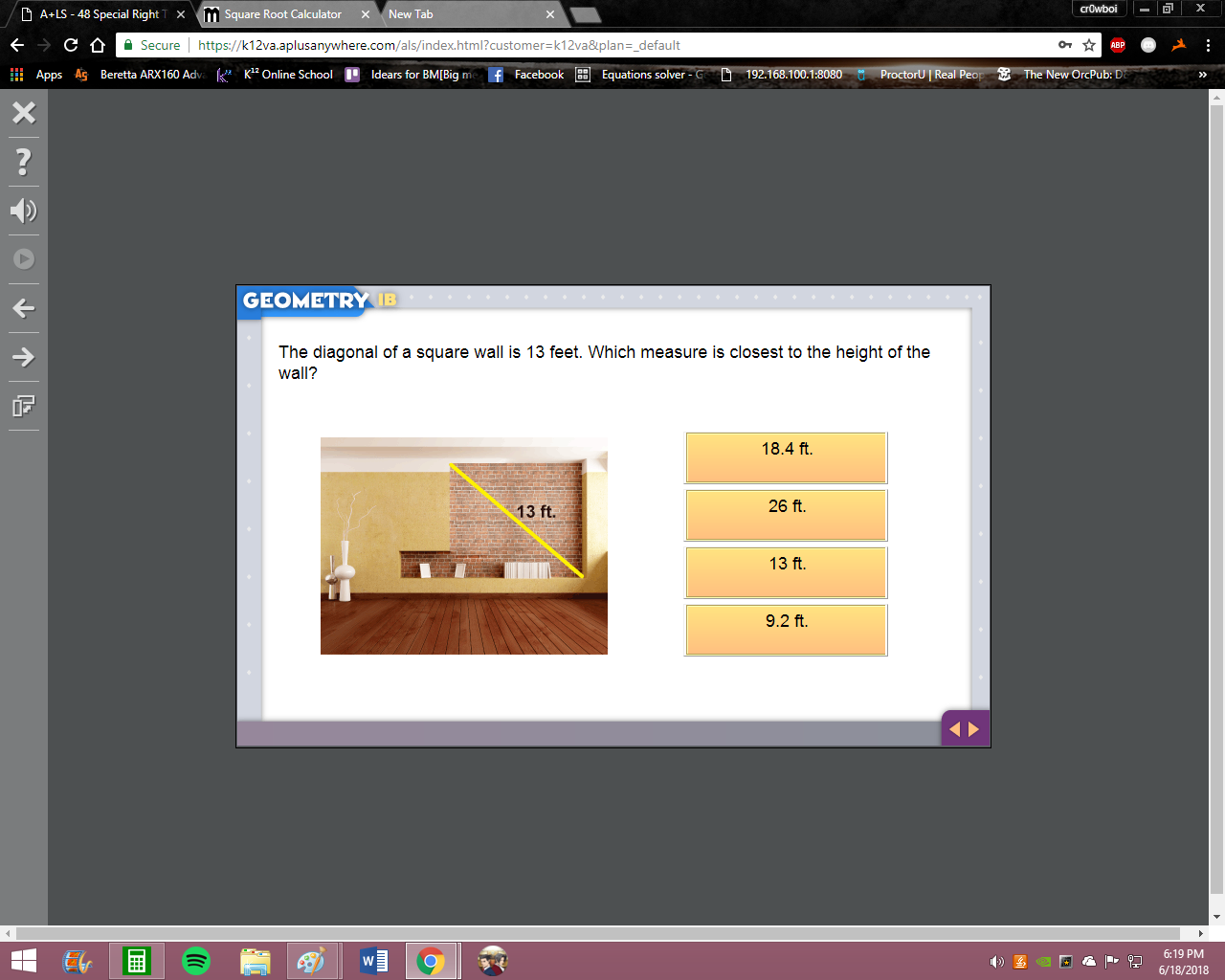
A?
The height of the wall is basically one leg of a right triangle so by definition it cannot be longer than the hypotenuse For a 45-45-90 triangle Leg = hypotenuse / sqrt(2) =?
I mean, even without doing any calculations there's only one choice less than the hypotenuse 13
9.2?
Yup good
the top right one?
Good
XZ
Hm that's a very good guess but XZ is the hypotenuse which is not considered a leg So between the other two sides which one do you think is longer?
XY
Good so xy is your sol 'n
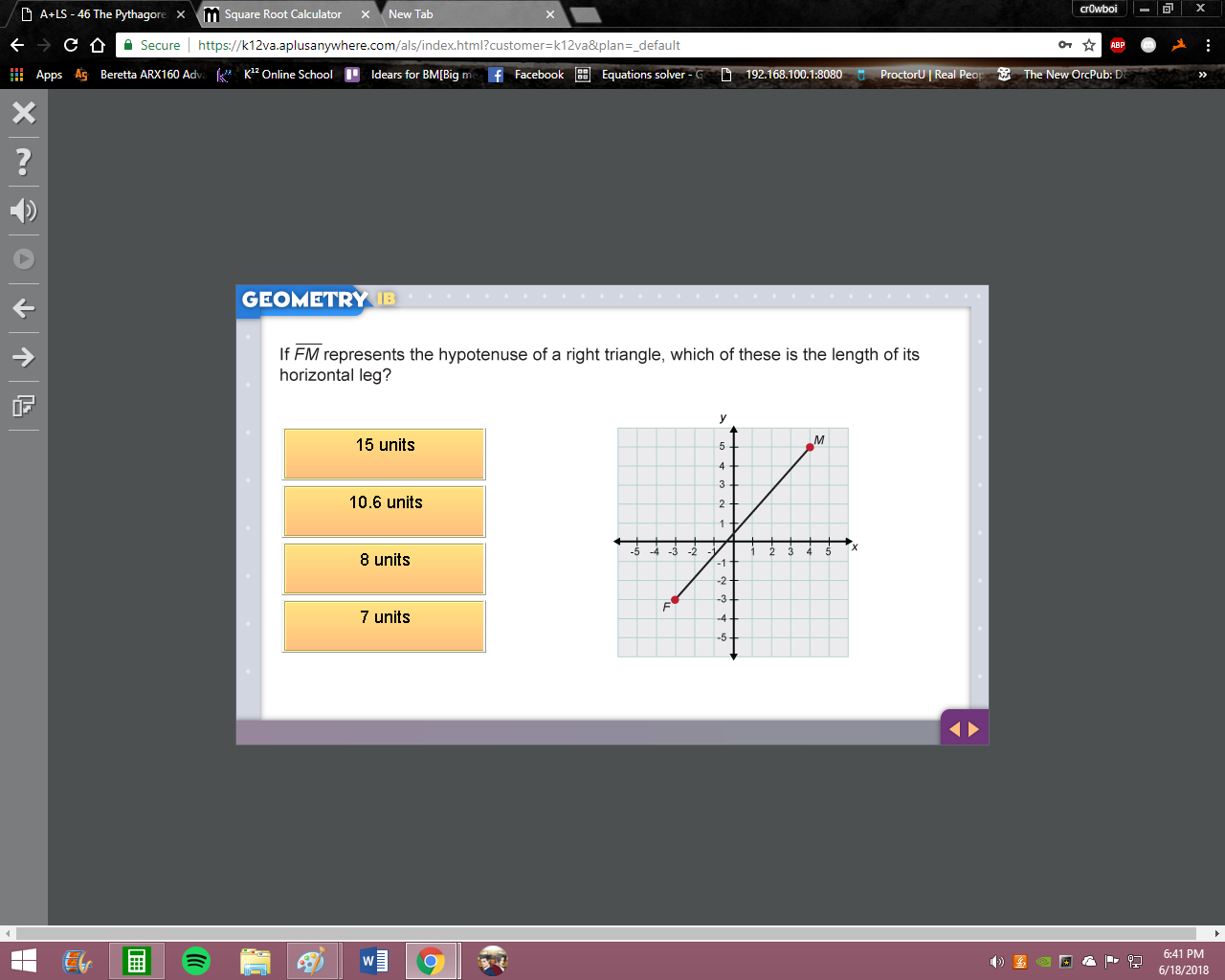
my choice is C
Hm not quite You're just gonna count the number of horizontal spaces between M and N
in other words just subtract the x-coordinates of M and N
* M and F I mean
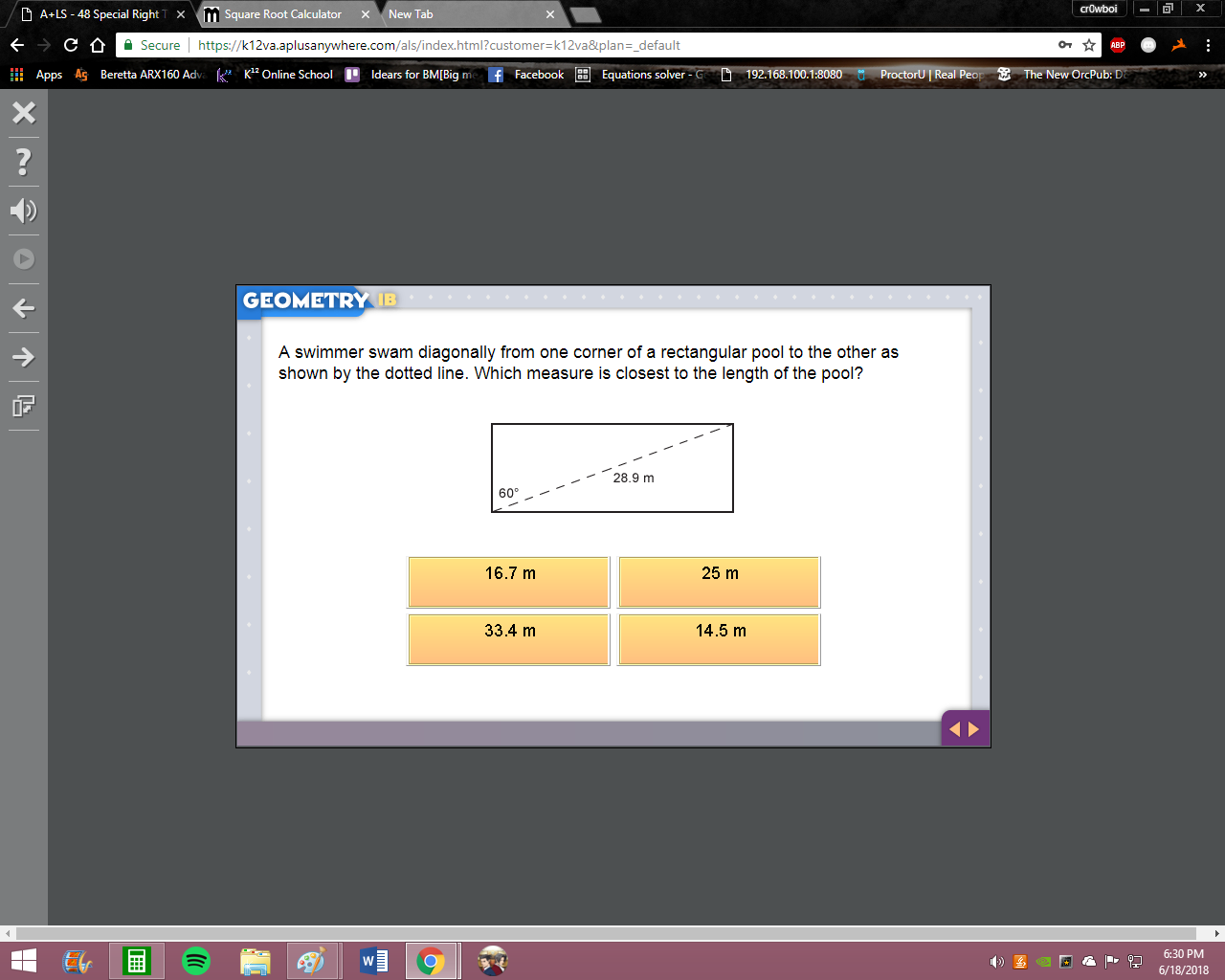
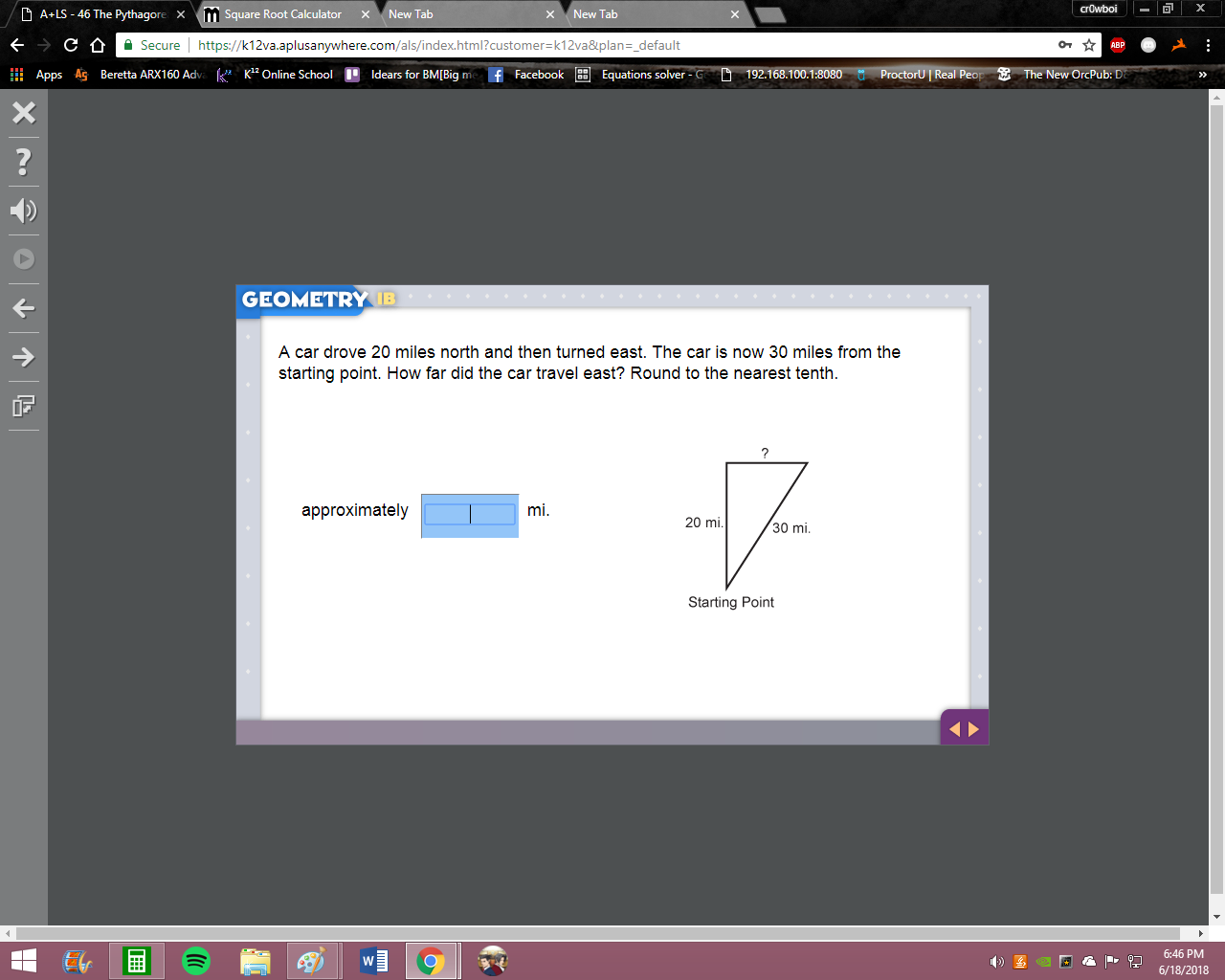
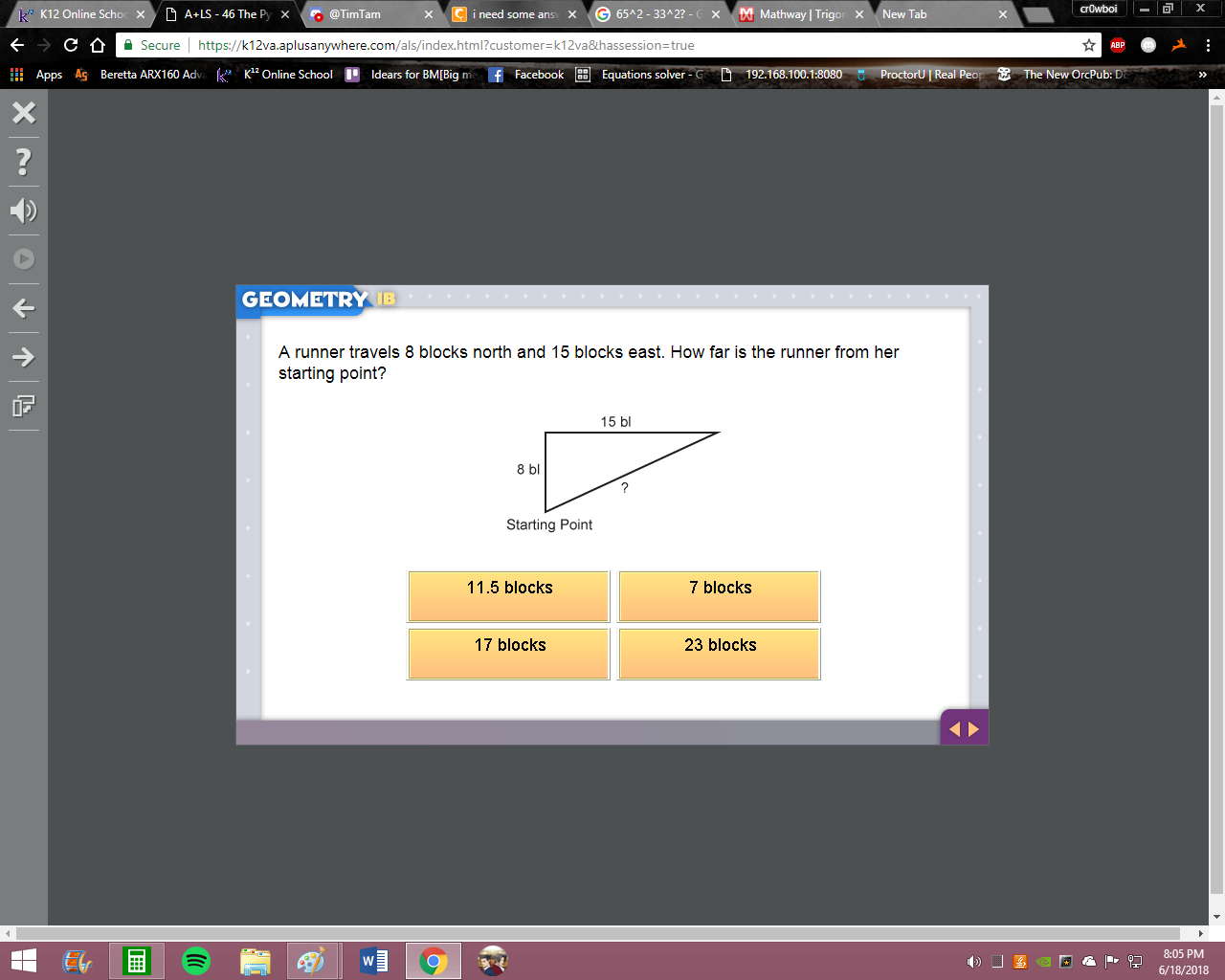
so you have a right triangle and you are given the hypotenuse and one leg so try plugging them into a^2 + b^2 = c^2 and solving for the missing leg
1300
36.05
hm, not quite, remember we have the hypotenuse (30) and one leg (20) so 30^2 = a^2 + 20^2 solve for a
500
almost, that's a^2 so you'd just have to take the square root of 500
22.3
almost, the square root of 500 is 22.360 something so it rounds up to 22.4 not 22.3
so thats my answer?
yes
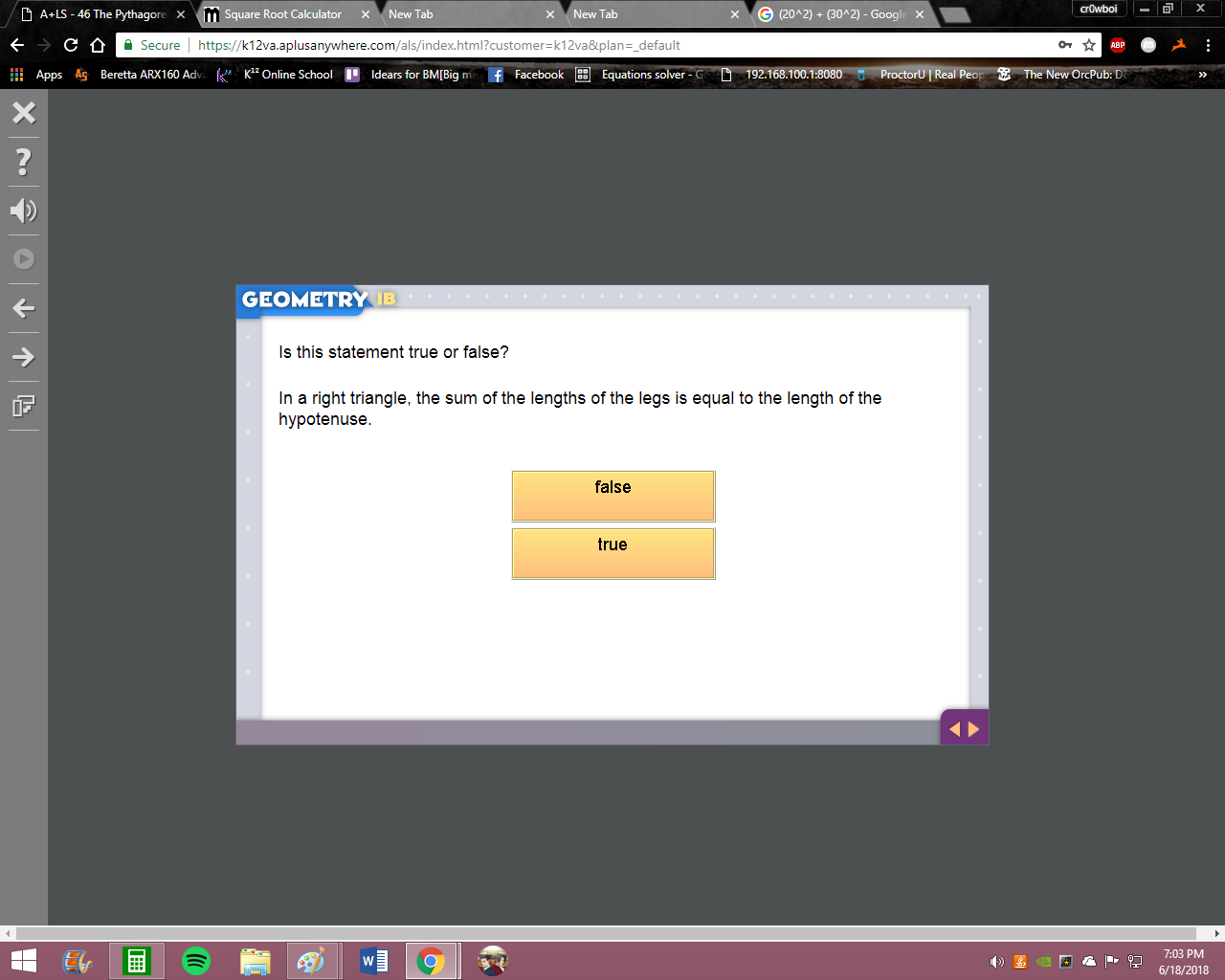
this is true
hm, be careful, it's the sum of the squares of the lengths, not just the lengths so false
the top right one
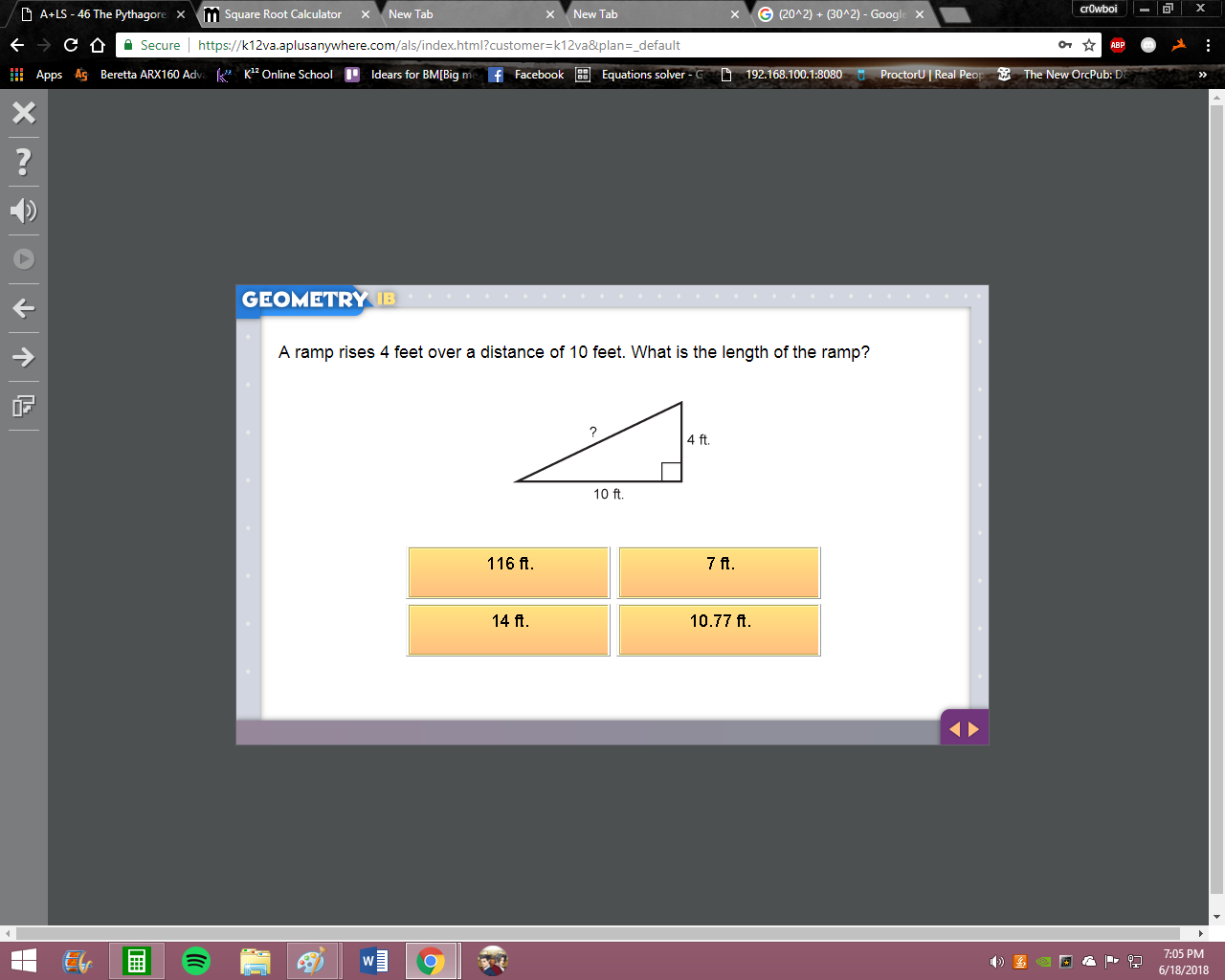
hm, not quite, a good thing to remember is that the hypotenuse is the biggest side so it has to be bigger than 10 a^2 + b^2 = c^2 plug in your legs (10 and 4) and solve for c
so the bottom left one? that's what i got from it
remember to square the sides before adding them 10^2 + 4^2 = ?
116
good and what's the square root of that?
i disconnected, sorry
10.7
good so 10.77 is the closest and thus your sol'n
24?
good
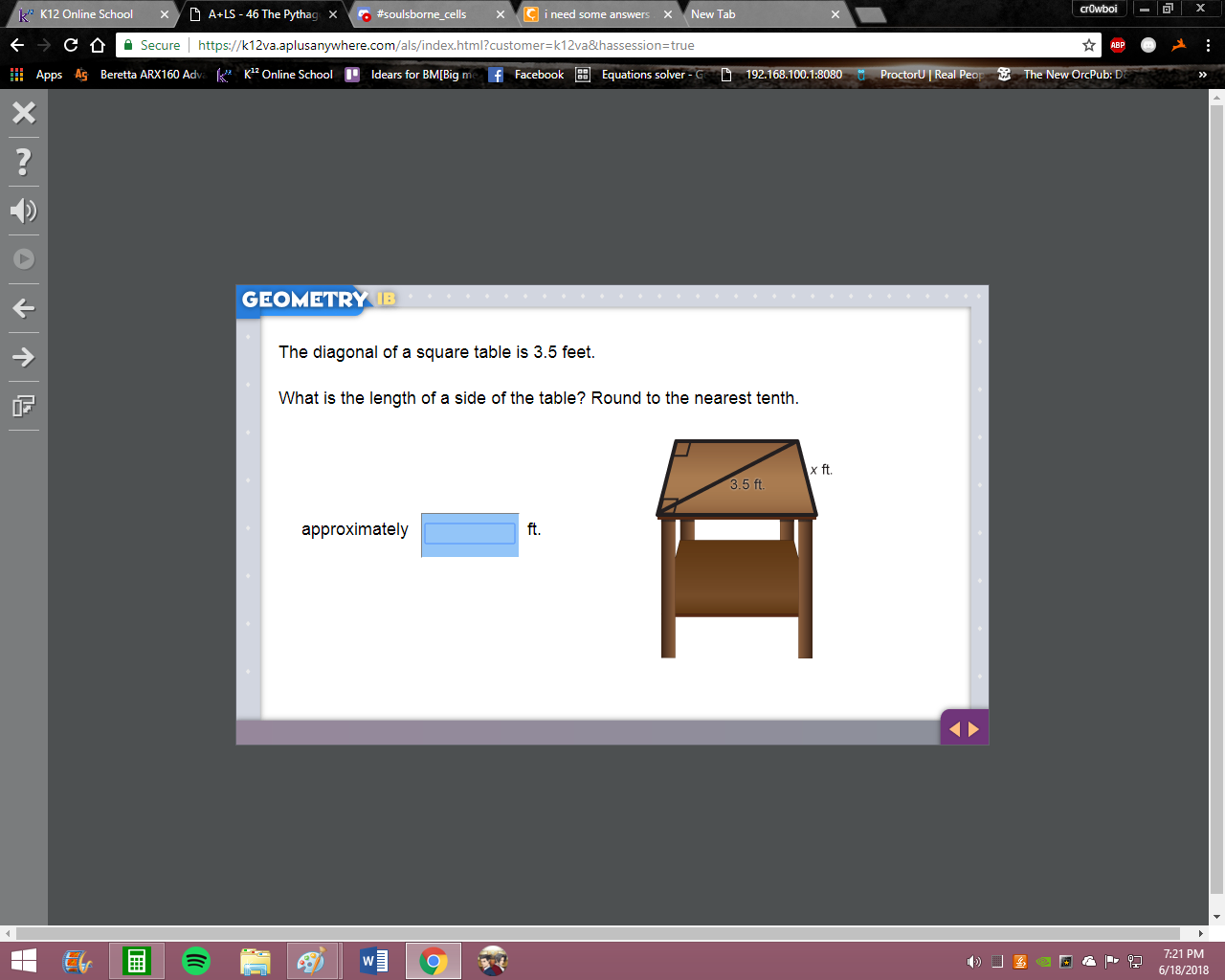
when you have a diagonal through a square you get two 45-45-90 triangles as usual leg = hypotenuse/sqrt(2) = ?
3.5?
12.25 i meant
hm not quite what is 3.5 divided by sqrt(2)? remember order of operations
I don't really know how to explain this any better haha you just need to type 3.5/√(2)
2.47
good but they want the nearest tenth so 2.5
7?
hm, not 7. remember you cannot just add the side lengths together, you have to use the formula a^2 + b^2 = c^2 to solve for c
when you sketched the triangle you got side lengths 3 and 4 right? plug those in as your a and b values then solve for c.
5
good so 5 = your sol'n
3?
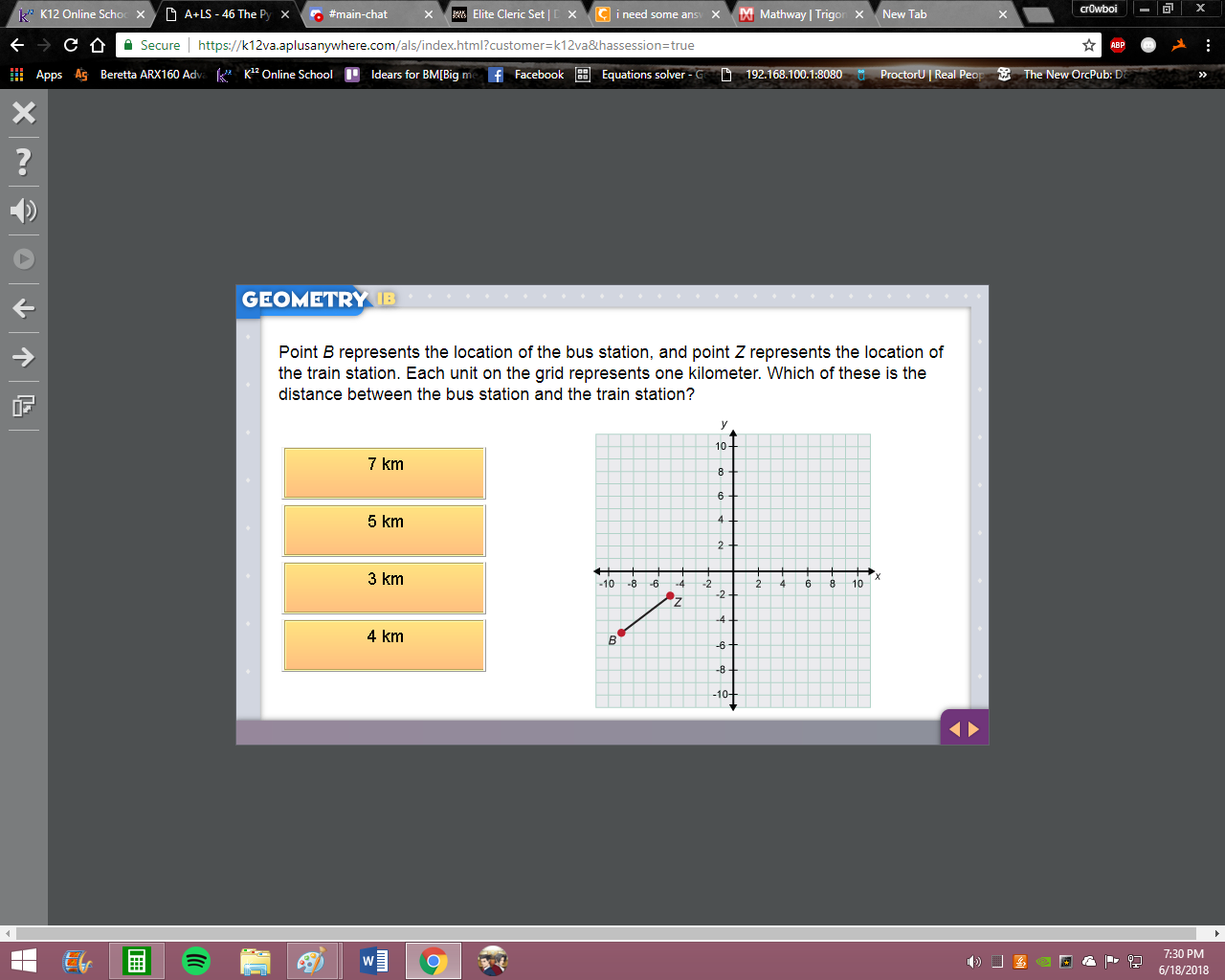
not quite what are the x-coordinates of B and Z?
-9 and -5
good so what's the difference of -9 and -5?
-4 apart?
good but since it's distance we take the absolute value of that to get 4 = your sol'n
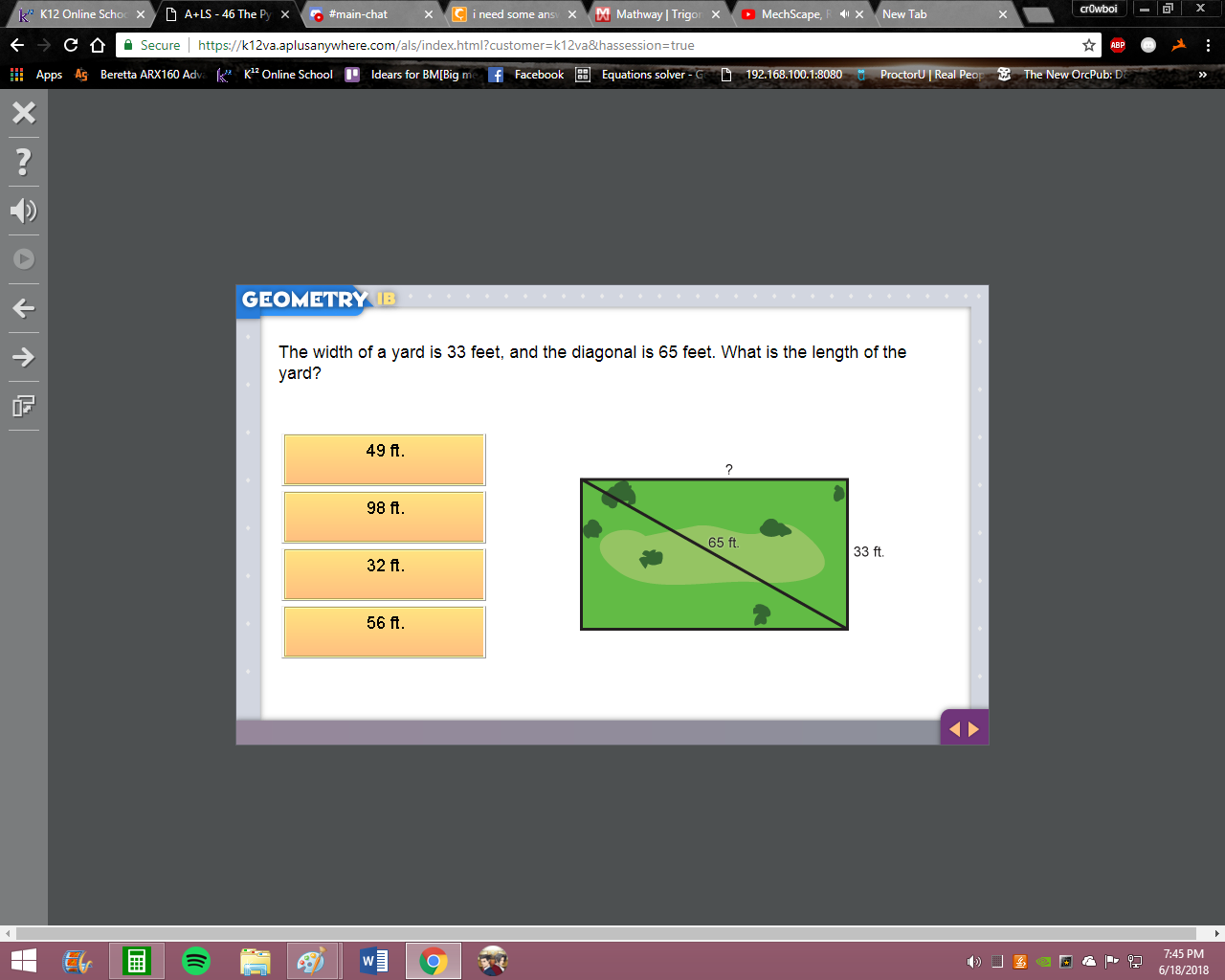
C?
not quite you are given the hypotenuse and one leg a^2 + b^2 = c^2 solve for the missing leg remember that c is the hypotenuse and (a and b) are the legs
the hypotenuse is 65 and one of the legs is 33 right? therefore 33^2 + a^2 = 65^2 so solve for (a)
49?
33^2 + a^2 = 65^2 subtract 33^2 from both sides to get a^2 = 65^2 - 33^2 therefore a = ?
5134
that's a^2 so if a^2 = 5134 a = ?
71.6
wait a minute how did you get 5134
what's 65^2 - 33^2?
65^2 = ? 33^2 = ? calculate the two values separately then subtract them
3136
56
good so 56 = your sol'n
17?
good
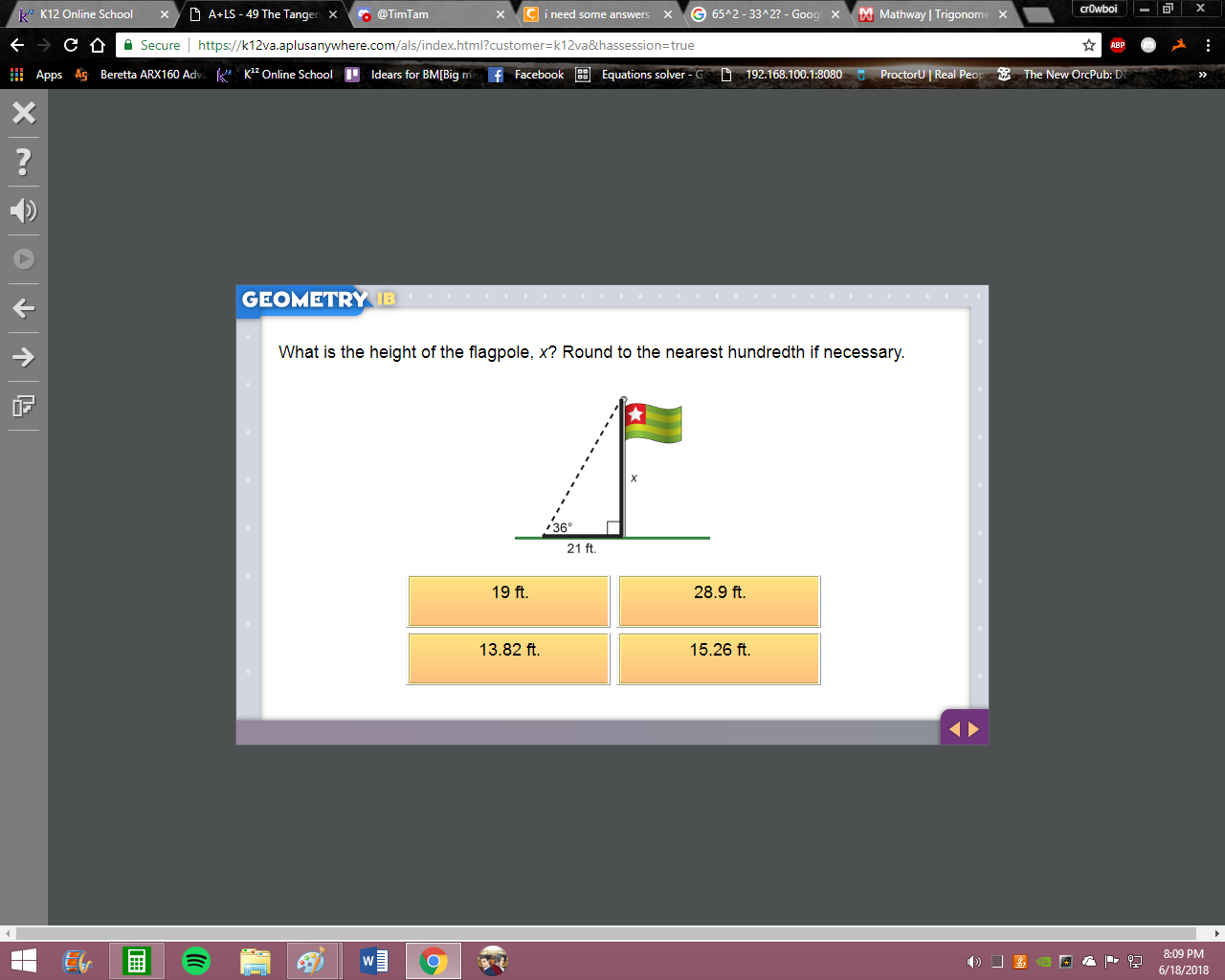
top right?
hm not quite you have the opposite and adjacent, what trig ratio is this?
uh...
dang, i just forgot trig...
|dw:1529378231682:dw|
as I stated before you have the adjacent and opposite sides which trig ratio is appropriate? check the diagram
which trig ratio involves the opposite and adjacent sides? check the red text
|dw:1529379233861:dw|
so you'd use tangent, right? so you set up tan(theta) = opposite/adjacent plug in your values & solve for the missing side.
i got top left, for some reason, i dont think its right...
which side of the triangle is opposite to the angle? and which is the adjacent side?
the dotted one is adjacent, right?
the dotted side is the hypotenuse and thus is not included in this calculation.
sorry, i'm not working at full capacity...
i'll keep trying though
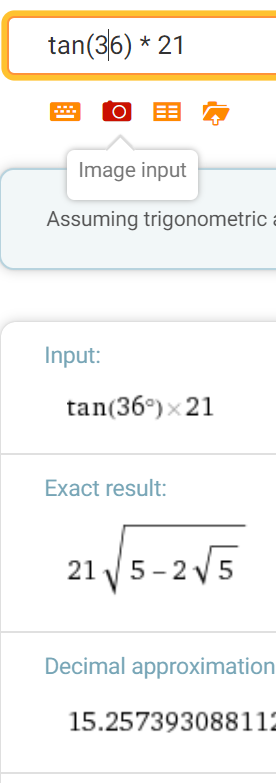
so there are only two other sides of the triangle are 21 and x notice how the x side is the farthest across from the angle, so that's our opposite side the 21 is next to the angle so that's our adjacent side therefore tan(36) = x/21 solve for x
i am so sorry, i passed out...
@Vocaloid let us continue where we left off
sure solving for x gives us tan(36) * 21 which you can then just plug into a calculator to get the sol'n
162
can you try putting in tan(36) then multiply the result by 21 ?
still 162
oh wait your calculator is probably in radians mode can you try changing it to degrees mode?
15.25?
good it rounds up to 15.26 actually so 15.26 is your sol'n
@Vocaloid
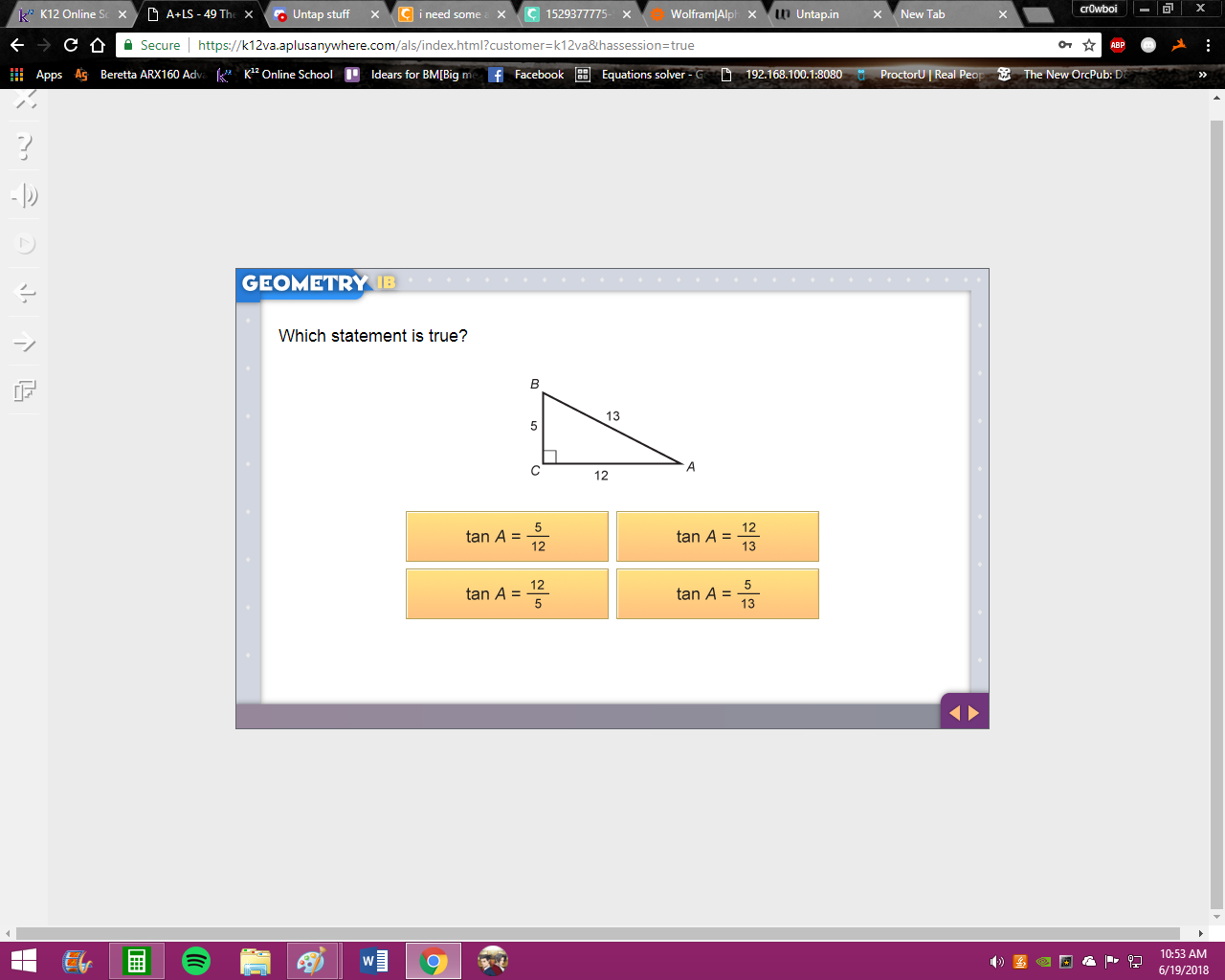
from the perspective of angle A opposite/adjacent = ? remember that the hypotenuse is not included
|dw:1529431215885:dw|
^ try to apply this logic to your triangle to figure out what the adjacent and opposite sides are remember that the opposite side is the furthest away from the angle, and the adjacent side is closest w/o being the hypotenuse
still there? try to see which side is farthest away from angle A and which one is the closest to angle A
yeah, thinking
i somehow got the bottom left one
that's the adjacent over the opposite tan is opposite over adjacent
the side farthest away from A is the 5 side the side next to A is the 12 side so opposite/adjacent = ?
\(\color{#0cbb34}{\text{Originally Posted by}}\) @Vocaloid ^ try to apply this logic to your triangle to figure out what the adjacent and opposite sides are remember that the opposite side is the furthest away from the angle, and the adjacent side is closest w/o being the hypotenuse \(\color{#0cbb34}{\text{End of Quote}}\)
therefore the opposite side is 5 and the adjacent side is 12 making tan = opposite/adjacent = 5/12 = your solution gtg
sorry , see you later
Join our real-time social learning platform and learn together with your friends!