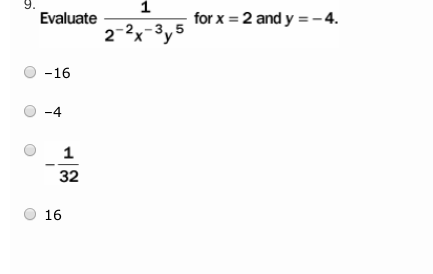Question

PLS HELP!!!

Answer 1

@Vocaloid

Answer 2

@mhchen

Answer 3

Substitute the x and y that were given

Answer 4

y=2, x=-4

Answer 5

Also
\(x^{-n}=\frac{1}{x^n}\)
n being any number

Likewise
\(\frac{1}{x^{-n}}=>x^n\)

Answer 6

Yes

Answer 7

\[\frac{ 1 }{ 4 }\]-\[\frac{ 1 }{ 64 }\],
32

Answer 8

That is confusing to look at
\(\large \frac{1}{2^{-2}x^{-3}y^5}\), \( x=2, y=-4\)

\(\large \frac{1}{2^{-2}2^{-3}-4^5}\)

\(\large \frac{1}{\color{red}{2^{-2}2^{-3}}-4^5}\) The red will flip to go on the numerator and will lose the - exponent

Answer 9

\[\frac{ 1 }{ 4 }\],\[\frac{ 1 }{ 8 }\],-1024

Answer 10

Also quick note, if you want to copy the latex, right-click the math and Show Math As > Tex Commands

When pasting include `\( \)` in between

Answer 11

@dude thanks
how do I get the final answer

Answer 12

\(\large \frac{1}{2^{-2}2^{-3}-4^5}\)

After flipping the numbers to the numerator
=\(\large \frac{2^{2}2^{3}}{-4^5}\)


\(2^2=4\)
\(2^3=8\)
and
\(-4^5=-1024\)

Answer 13

\(\large \frac{4\cdot 8}{-1024}\)

=\(\large -\frac{32}{1024}=>\boxed{\frac{1}{32}}\)

Answer 14

@dude pardon but the result is minus 1/32

Answer 15

@ThisGirlPretty do you agree it ?

Answer 16

Right, thank you
\(\large -{\frac{1}{32}}\)

Answer 17

Match the approach to the treatment described
Question 39 options:

Herbie is displaying anxiety when he drives.

Answer 18

math help, screenshot in comments

Answer 19

Which scale factors produce a expansion under a dilation of the original image?

Select each correct answer.

Answer 20

Systematic Desensitization

Electroconvulsive therapy (if all other treatments have failed)

Lithium Carbonate (medication)

Anti-psychotic drugs and then p

Answer 21

A plane intersects a pentagonal pyramid horizontally as shown. Describe the cross-section.

Answer 22

Including details about a person's experience in an essay

creates sympathy

enga

Answer 23

Phineas Gage suffered a serious brain injury when a rod went through his brain. T

Answer 24

math help, pic in comments

Answer 25

How does the activity in this image represent specialization?
A) The products being produced are specialized for each worker.

Answer 26

Average Travel Time to Work
(Workers 16 years and over who did not work at home- in minutes)

New York City, NY: 38.

Answer 27

math help, pic ion comments

Answer 28

According to this graph, most of immigrants to Europe come from
A) the Caribbean.

Answer 29

math help, pic in comments

Answer 30

Solve for X

Answer 31

Which of these would be MOST LIKELY to be considered a geographic "push factor"?

Answer 32

In terms of ethnicity, both the United States and Switzerland
A) have no ethnic controversies.

Answer 33

Math help please

Answer 34

How did the area known as the "Ring of Fire" earn its nickname?
A) Solar eclipses are visible in the area.

Answer 35

The spread of ideas, art, religions, technologies, and languages from one culture to another is known as
A) voluntary trade.

Answer 36

math help, pic in comments