Question

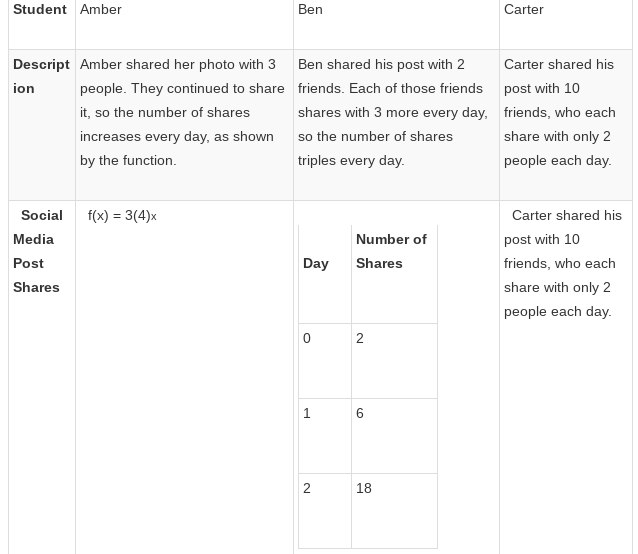
Algebra FLVS 3.04

Answer 1

Write an exponential function to represent the spread of Ben's social media post.

Write an exponential function to represent the spread of Carter's social media post.
Graph each function using at least three points for each line. All graphs should be placed together on the same coordinate plane, so be sure to label each line. You may graph your equation by hand on a piece of paper and scan your work, or you may use graphing technology.
Using the functions for each student, predict how many shares each student's post will have received on Day 3 and then on Day 10. Justify your answers.
If Amber decides to mail copies of her photo to the 45 residents of her grandmother's assisted living facility, the new function representing her photo shares is f(x) = 3(4)x + 45. How does this graph compare with the original graph of Amber's photo share?
Based on your results, which students' post travels the fastest? How is this shown in the equation form of the functions?
If you had to choose, would you prefer a post with fewer friends initially but more shares, like Amber, or more friends initially but fewer shares? Justify your answer with your calculations from previous questions.

Answer 2

@DCharger96 @dude

Answer 3

im no good math i can't math

Answer 4

DC, do you know anyone who is??

Answer 5

i might

Answer 6

@121314gifted

Answer 7

I have found out that the Ben's is f(x)=2(3)^x and Carter's is f(x)=10(2)^x and I graphed them. I'm having a hard time finding out what they will be at day 10

Answer 8

Just give me a few more minutes and I'll have it for you

Answer 9

Ok thank you

Answer 10

1. Based on other resources, Ben initially shares a post with his 2 friends and the shares grow by a rate of 3 shares per person per day. Based on this information, we can write it in the following function: where x is the number of days.2. Carter, on the other hand, shares a post with 10 of his friends and the shares grow by a rate of 2 shares per person per day. Putting this into an exponential function, we'll get: where x is the number of days.3. To solve this, we first need to know that the third student, Amber, shares a post with 3 of her friends and her shares grow by a rate of 4 shares per person per day. This means that her function is: where x is the number of days.Refer to the attachment for the graph of the functions of Amber, Ben, and Carter. The red line shows Amber's graph, the blue line represents Ben's, while the green line shows Carter's.4. To find how many shares each student will receive on day 3 and day 10, we just substitute 3 and 10 respectively for the value of x since we have previously defined that x represents the number of days and f(x) are the functions of the shares the students got.For Amber:Amber will have 192 shares by Day 3 and 3,145,728 shares by Day 10.For Ben:Ben will have 54 shares on Day 3 and 118,098 on Day 10.For Carter: Carter will have 80 shares by Day 3 and 10,240 by Day 10.5. If Amber's graph were to be changed to , then this new function will still have the same curve as Amber's original function but this new graph will just be translated 45 units above.6. By looking at the graphs of the shares of the three students per day, we can see that Amber's posts travel the fastest. This is because, in exponential functions, the base influences the rate of growth of the function. Since Amber's function had the greatest base which is 4, her shares will have the highest growth rate.7. I would want my posts to spread faster therefore I would prefer having fewer friends initially but more shares. This is because of the same explanation stated in number 6. It will not matter how many friends you have initially when the growth of your shares is slow. This is evident from the graphs of Amber, Ben, and Carter. Amber's shares, which has the situation I prefer, travels the fastest even though Carter initially had more friends

Answer 11

Thank you!

Answer 12

Thanks DC.

Answer 13

np

Answer 14

Thanks 121314gifted!!!