Question

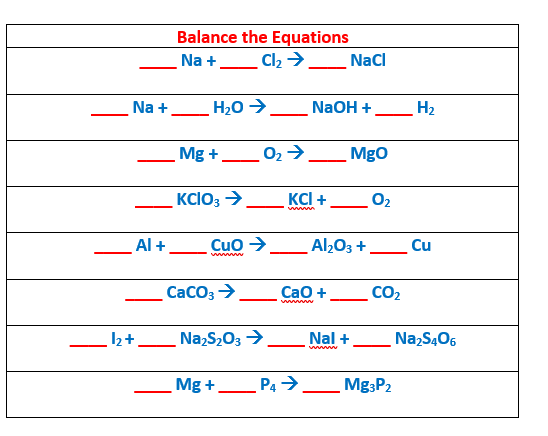
If you know how to balance equations can you help me out with this?

Answer 1

So do you need a walkthrough or do I just do them?

Answer 2

Oh yes, I love balancing equations, even simple and hard ones in chem. I've gotchu

Answer 3

Oh these are simple, not like balancing redox reactions. I'll do a couple of unique ones to get you started

1.
Na+ Cl2 -> NaCl
There's 2 Cl so you need to multiply the product by 2
Na + Cl2 -> 2NaCl
Now you have 2 Na, so you need to balance that on the left side
\(2Na + Cl_2 \rightarrow 2NaCl\)

2.
Na + H2O -> NaOH + H2
You have 1 Na on each side √
You have 1 O on each side √
You have 2 H on the reactants and 3 on the products. Odd coefficients are annoying, so you'd need to multiply both to reach an even number. I'd multiply NaOH twice to have 4 H's on the products.
Na + H2O -> 2NaOH + H2
You have 4 H's on products, you need to have 4 on the reactants
Na + 2H2O -> 2NaOH + H2
Now you have equal number of H's on each side. However you now have 2 Na's on the products and 1 on the reactant, so you must multiply the reactants by 2
\(2Na + 2H_2O \rightarrow 2NaOH + H_2\)
You have 2 Na on both sides √
4 H on both sides √
2 O on both sides √



#3 is much like #1. You have a metal reacting with a diatomic, so it will be the same. The nice thing about such reactions is that if you are familiar with the coefficients of a few reactions, you can apply it to others.

#4 is a decomposition reaction. It works much like #3 and #1 except it's opposite and you might have slightly different coefficients


I'll skip straight to #6, because there's a polyatomic ion

\(CaCO_3 \rightarrow CaO + CO_2\)
\(CO_3^{2-}\) is a polyatomic ion which can be considered as its own. However, this reaction in particular is a decomposition reaction of Calcium carbonate. But the number of Ca, C, and O's are the same on the reactants and products, so it is already balanced.

#7 looks very interesting. It's a redox reaction probably, but you would not need to balance it the half reaction method.

\(I_2+Na_2S_2O_3 \rightarrow NaI + Na_2S_4O_6 \)
A helpful tip if you have some atoms showing up twice (kind of like #2) is to try and first balance components that only appear once, so that you don't get confused. I'll balance Iodine by multiplying the product NaI twice
I2 + NA2S2O3 -> 2NaI + Na2S4O6
Now there's 2 Na in the reactants and 4 in the products, so I'd multiply the reactants twice
\(I_2 + 2NA_2S_2O_3 -> 2NaI + Na_2S_4O_6\)
Now this has automatically balanced # of S and # of O on each side


Now you can try and continue the rest. Hopefully these are enough to start you off.

Answer 4

So there's an algebraic approach to doing this, believe it or not. First, take note of your elements and how many of them there are. Then, we just assign each of the varying elements with variables. So let's do the first one with said method.
Let's assign Na with the variable of x, and Cl with the variable of y. Now, we must separate each of these out so that way the corresponding variables line up with each other. This is where counting how many of each element comes into play.

\[1x = 1x\]
\[2Y = 1\]

Now that we have our equations set, we shall solve them.
X is equal to 1, and Y is equal to 1/2
Therefore, our equation would look like
\[1Na + 1/2Cl_{2} = 1NaCl\]
Now because we cannot have a coefficient of 1/2, we simply multiply both sides by 2 to get
\[2Na + 1Cl _{2} = 2NaCl\]

Answer 5

Also, I stated this badly, so let me fix my error from my previous post. The variables are used to represent the different terms of each coefficient. The coefficient of each variable will represent the number of elements. and the elements themselves But you will create equations with the corresponding elements. So let's try a hard one with this method. Let's do
\[I _{2} + Na _{2}S _{2}O _{3} = NaI + Na _{2}S _{4}O _{6}\]
Lets assign the first term with w, second term with x, third term with y, and fourth term with z.
\[2W = 1Y\] This equation represents all of Iodine elements in the chemical equation, with them being represented as first and third terms.
\[2X = 1Y + 2Z\] This equation represents all of the sodium elements, with them being represented as second, third, and fourth terms.
\[2X = 4Z\] This equation represents all of the sulfur elements, with them being represented by the second and fourth term.
\[3X = 6Z\] This equation represents all of the oxygen elements, with them being represented in the second term and fourth term.

Note how there are 4 equations, as there are 4 elements. To reiterate, the 4 different equations are used to quantify the number of unique elements present in our chemical equation, while the variables represent the coefficient of the terms we plug into our chemical equation. Now this is where we have a puzzle. You may be wondering how we solve this, not knowing anything. Well there is an easy way out of this. Assume that one of the variables equals 1. Preferably, assign this value to the unknown variable that appears the most. For now, let us assume that x = 1. Knowing this, we can start solving our equations. Because we know x = 1, we can find y this way with the third and fourth equation. This is what we know because of that:
X = 1
Z = 1/2

Now we are simply missing W and Y. Let's find them with our second and first equation, but starting off with the second equation.
By plugging in 1 for x and 1/2 for z, we find that:
Y = 1

Now we return back to the first equation. We plug in our y value to get:
W = 1/2

Again, since we can only have integer coefficients, we multiply each coefficient by 2 to get
W = 1
X = 2
Y = 2
Z = 1
Therefore, the equation is
\[I _{2} + 2Na _{2}S _{2}O _{3} = 2NaI + Na _{2}S _{4}O _{6}\]

Answer 6

This method does take quite a while to wrap your head around, but this is the definitive way to never guess and check chemical equations and head straight for the answer.