Question

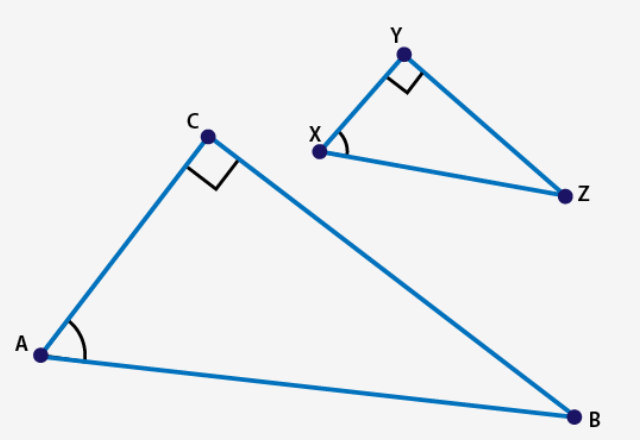
Triangle XYZ was dilated by a scale factor of 2 to create triangle ACB and sin ∠X = 5 over 5 and 59 hundredths.

Part A: Use complete sentences to explain the special relationship between the trigonometric ratios of triangles XYZ and ABC. You must show all work and calculations to receive full credit.

Part B: Explain how to find the measures of segments CB and AB. You must show all work and calculations to receive full credit.

Answer 1

ok so like a first step how you think what mean a dilation by a scale factor of 2 ?
for example a length of 1 unit how many will be ?

Answer 2

@supie

Answer 3

What exactly do you mean? Are asking what I think a dilation of two is?

Answer 4

yes ofc

Answer 5

Well a dilation is when the triangle is made bigger by a number/ratio, in this case 2, as long as you dilate by the same number all the triangles are proportionate.

Answer 6

ok but i ve asked you a little simple question

what mean a dilation by two ? with this example pls.

Answer 7

@Laylalyssa why is this so difficile to answer ?

Answer 8

\(\color{#0cbb34}{\text{Originally Posted by}}\) @jhonyy9
@Laylalyssa why is this so difficile to answer ?
\(\color{#0cbb34}{\text{End of Quote}}\)
difficult*

Answer 9

Well the scale factor of 2 was used to dilate triangle XYZ into triangle ACB?

Answer 10

Well I guess he gave up, does anyone know how to do this?

Answer 11

@jhonyy9 are u gonna finish☔️

Answer 12

So lets explain the special relationship between the trig ratios of XYZ and ABC, if you know what a ratio is, we can do this pretty easy. A dilation just means increasing (or decreasing) all sides by the same scale factor, when we do this we can find a ratio between corresponding side lengths on both triangles, For example If I have a triangle here
(assume both triangles are similar, and the bigger triangle is dilated by a factor of 2, meaning all sides are twice as big,) we can set a ratio comparing the small triangle to the big one, which would be 1:2 in the case we just discussed. (btw this is all background not answering the question just yet). Since in your problem we are dilating by a scale factor of 2 we can find the trig ratios of both triangles

Answer 13

Now getting into the meat of this, "Triangle XYZ was dilated by a scale factor of 2 to create triangle ACB and sin ∠X = 5 over 5 and 59 hundredths."
we need to explain the trig ratios between the 2 triangles
we are given "sin ∠X = 5 over 5 and 59 hundredths"

Answer 14

Lets start out by drawing an angle x, this angle will be opposite the side length of 5 and the hypotenuse will be 5.59
Tthis is because sin is \[opposite/hypotenuse\]

Answer 15

It does provide an image, but I'm not sure how to make it into a file.

Answer 16

now that was for triangle XYZ, so side X = 5 (because the side is named opposite of the angle,) also the image doesnt really matter its fine because you just need to visualize it.

Answer 17

Actually for your image is y the hypotenuse or z???

Answer 18

Y is the right angle so I would suppose z is the hypotenuse.

Answer 19

this is the drawing then, that we will refer too

Answer 20

Ok, so really the next thing we want to do is find the side length z, can you do taht?

Answer 21

Probably not

Answer 22

ugh I was being dumb, it does not specifiy if this was a right triangle. Is it?

Answer 23

Sorry its only in anything math related that I'm completely useless

Answer 24

no no no, ur doing fine. In the drawing is the triangle a right triangle?

Answer 25

No, its not a right trangle.

Answer 26

smh ok now the approach to that is the triangle i gave you before, just imagine its like a bit off or something (not a right triangle). So from here we need to use law of cosine. Do you know this?

Answer 27

I don't think I've ever heard of it.

Answer 28

Ok yeah I'm hopeless, thank you for staying patient with me.

Answer 29

hmm, this is super confusing if you havent heard of the rule, also super weird because if this triangle isnt a right triangle then we cant use pythagorean theorem, at this point seeing the picture might help. Click the attach file button right below

Answer 30

But it isn't a file, and I dont know how to make it into one.

Answer 31

you can screen shot it., crop out whatever you need to crop out and then attach as a file

Answer 32

Is there another to screenshot other than clicking prt sc?

Answer 33

not sure what ur talking about... you should be able to screenshot, save the SS (which might automatically do) then click the button and upload the SS

Answer 34

The problem is, I don't know how to screenshot

Answer 35

As I was saying, completely hopeless.

Answer 36

I even managed to lose my headphones, and I had just found them yesterday *face palm*

Answer 37

asdfghjkl,
search it up on google, type in how to SS on *insert device name here*

Answer 38

Hey I got it!

Answer 39

alr, hold on 10-15 min

Answer 40

Yes, sorry for taking so much of your time already.

Answer 41

oh breh that actually is a right triangle
XD

Answer 42

ok, we dont gotta go into the law of cosine junk xD,
for an fyi, if a triangle has a box, it means it is a right triangle, as u can see in that pic

Answer 43

\(\color{#0cbb34}{\text{Originally Posted by}}\) @darkknight
Ok, so really the next thing we want to do is find the side length z, can you do taht?
\(\color{#0cbb34}{\text{End of Quote}}\)
pythagorean theroem
\[x^2+z^2=y^2\] (y is hypotenuse)
\[5^2+z^2=5.59^2\] solve for z

Answer 44

Oh...woops

Answer 45

*facepalm* lol ur good, can u find z?

Answer 46

I..dont think so

Answer 47

\[z^2=5.59^2-5^2\]
\[z=\sqrt{5.59^2+5^2}\]
solve for z?

Answer 48

7.49 rounded to 7.5?

Answer 49

SMH SMH SMH
I meant \[z = \sqrt{5.59^2-5^2}\]
very sorry

Answer 50

Oh thats fine

Answer 51

2.5 then?

Answer 52

umm if u did the math right it should be right, now the rest is pretty easy
we need to find the trig ratios
Lets say sinx = 5/5.59
guess what?
sin(a) also equals 5/5.59 !!!
This is because we dilated, sin is a ratio, since the ratio of the 2 triangles are the same, for corresponding angles the sin ratio, the cos ratio, tan ratio, etc. will be the same for angle X and angle A, likewise for the other angles. Tis is part 1 so use like another example maybe with respect to another variable like z and b. On the smaller triangle we found every side length, since the bigger triangle is just twice that we can solve part 2 but just multiplying the corresponding side on the smaller triangle by 2

Answer 53

Sorry I'm just trying to figure out what to write exactly.

Answer 54

Ok so would the answer
There is a relationship between the triangles because of the dilation of 2

z=square root 5.59squared−5squared

z=square root (559/100)squared-25

z=2.49

Round up and you get 2.5

sinx=5/5.59 and sin(a) is also 5/5.59

This is because we dilated, sin is a ratio, since the ratio of the 2 triangles are the same, for corresponding angles the sin ratio, the cos ratio, tan ratio, etc. will be the same for angle X and angle A, likewise for the other angles. If you find the side lengths for triangle XYZ you are able to know the side lengths of ACB by multiplying them by 2 since it was dilated by a scale factor of 2.

Answer 55

For part A

Answer 56

im back, hold on a moment

Answer 57

\(\color{#0cbb34}{\text{Originally Posted by}}\) @Seafoam
Ok so would the answer
There is a relationship between the triangles because of the dilation of 2

z=square root 5.59squared−5squared

z=square root (559/100)squared-25

z=2.49

Round up and you get 2.5

sinx=5/5.59 and sin(a) is also 5/5.59

This is because we dilated, sin is a ratio, since the ratio of the 2 triangles are the same, for corresponding angles the sin ratio, the cos ratio, tan ratio, etc. will be the same for angle X and angle A, likewise for the other angles. If you find the side lengths for triangle XYZ you are able to know the side lengths of ACB by multiplying them by 2 since it was dilated by a scale factor of 2.
\(\color{#0cbb34}{\text{End of Quote}}\)
exactly this, part 1 done, but now for part 2 "Part B: Explain how to find the measures of segments CB and AB. You must show all work and calculations to receive full credit.

" you have to actually find CB and AB, can u do that now?

Answer 58

I don't think so.

Answer 59

CB is just side x times 2... you are already given side x's length, multiply by 2 to get CB
for AB take its corresponding side and multiply by 2

Answer 60

I see the concept, but what are the side lengths for the triangle?

Answer 61

Sorry I left for so long, I had to complete my DBA

Answer 62

look at the earlier drawings, we wrote out x and y and solved for z. everything is given already

Answer 63

Ok so z is 2.5 but where was x and y said?

Answer 64

And is z really a side length? It looks like its written at the angle.

Answer 65

\(\color{#0cbb34}{\text{Originally Posted by}}\) @darkknight
Created with Raphaël 2.0.2Reply Using Drawingthis is the drawing then, that we will refer too
\(\color{#0cbb34}{\text{End of Quote}}\)
@seafoam the lowercase are the angles, and the sides opposite it are sides
X, Y, Z are sides. x, y, z are angles