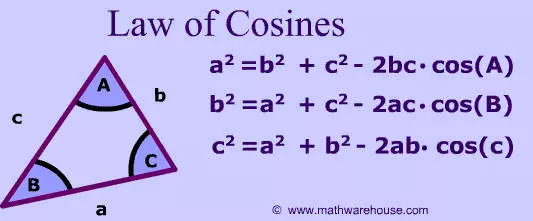Question

In triangle LMN, LM = 6, MN = 9, and LN = 7. Find m∠M to the nearest tenth of a degree.

A. 50.0 degrees
B. 41.8 degrees
C. 45.5 degrees
D. 87.3 degrees

Answer 1

Do you know the law of cosine? @Therndon50

Answer 2

a little

Answer 3

@AZ

Answer 4

So if know three sides, we can find the angle of one of them

Answer 5

Take a look at the formula

Answer 6

Do you think you can set up the formula to find the angle M for our question?

Answer 7

Not really @AZ

Answer 8

Thank you for the formulas @AZ

Answer 9

You don't have to tag me each time :) I get a notification whenever you respond to the post!

Answer 10

so if you look at the formulas,

if we're trying to find an angle like M, then we use the formula that has the side opposite to it

so in our case, we'll have

(LN)^2 = (LM)^2 + (MN)^2 - 2*(LM)*(MN)*(cos M)

and we already know from the question

LN = 7
LM = 6
MN = 9

Answer 11

Does that make sense? Can you plug in the numbers now

Answer 12

Yes, I just can't figure out what cosine to use

Answer 13

what do you mean?

first let's simplify all the numbers and then we can solve for M

once you get to
cos M = some number

we have to do the inverse of cos
on your calculator, it can be written as cos^-1 or as arccos

Answer 14

so

cos M = some number

then on your calculator
arccos (some number) = the angle M

Answer 15

so let's plug in your numbers, shall we?

7^2 = 6^2 + 9^2 - 2*(6)*(9)*(cos M)

can you simplify it?

what is 7^2 =
6^2 =
9^2 =

Answer 16

I dont think I'm setting the equation right

Answer 17

I got an answer of 59.1

Answer 18

mhmm if you want, we can go through it step by step

or if you show me your work, I can try to find out where you went wrong

Answer 19

ok I tried it again, I got 50.1

Answer 20

is that close?

Answer 21

Now that is the correct answer!

Answer 22

ok Thank you so much

Answer 23

I guess in your answer choices, they somehow must have rounded off in one of the earlier calculations to end up with 50.0

Answer 24

Of course! I'm glad you were able to solve it!!

Answer 25

@Therndon50 since your done and you have your answer Please Close this post