Question

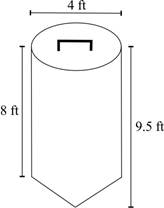
A company that manufactures storage bins for grains made a drawing of a silo. The silo has a conical base, as shown below:

The figure shows a silo shaped as a closed cylinder with a conical end. The diameter of the silo is 4 ft, the length of the cyl

Which of the following could be used to calculate the total volume of grains that can be stored in the silo? (6 points)

π(2ft)2(8ft) + one over three π(2ft)2(9.5ft − 8ft)
π(8ft)2(2ft) + one over three π(2ft)2(9.5ft − 8ft)
π(2ft)2(8ft) + one over three π(9.5ft − 8ft)2(2ft)
π(8ft)2(2ft) + one over three π(9.5ft − 8ft)2(2ft)

Answer 1

omai that's a lot of 🥧

Jokes aside, the volume of a cylinder usually operates off this formula:\[V_{cylinder}=\pi r^2h\]and the volume of a cone usually operates off this other formula:\[V_{cone}=\frac{1}{3}\pi r^2h\]To get a "conical cylinder" (i.e. the whole shape of your silo here) we would use either this unnecessarily complicated format or the ultimate formula below:\[\Large{V_{silo}=\pi r^2h+\frac{1}{3}\pi r^2h}\]

Answer 2

omg

Answer 3

Indeed, a lot of 🥧

Answer 4

I cant lol

Answer 5

Is the answer B?

Answer 6

There was so much that I walked in the door and got pied immediately. 😩

Answer 7

because thats what I got

Answer 8

...hold on I have to parse the question... why is it phrased so complicated? 💀

Answer 9

So this is what you're given and they expect you to calculate a whole volume formula off this? Smh

Answer 10

what 8?

Answer 11

Oh wait I forgot the other part. The length of the cylinder is also the diameter. GotchaNo idea what the cone's height is though

Answer 12

Are there any other values given? It looks like your question got cut-off here

Answer 13

im sorry, I didn't pout the picture up

Answer 14

OOH. Okay that helps a lot. Except that is one weirdly shaped silo... when do the cones point down?

Anyway... back to the pie party.

Answer 15

So we have the diameter as 4 feet, the cylinder height as 8 feet and the silo's height as 9.5 feet.

First let's convert the diameter value into a format suited for the area of the base. The silo has only one base shape (a circle) that goes with both the cylinder and the cone, so:
Our radius will be half of the diameter, or \(r=2ft\). So the base should be \(B=\pi(2ft)^2\)

Moving on, we look at the volumes of each section of the silo.
The cylinder's height, as previously stated, is \(8ft\) so the volume should be\[V_{cylinder}=\pi(2ft)^2(8ft)\]As for the cone, we don't have the exact height for that but we can calculate it! You have the full silo height and the cylinder's height, so a little subtraction should work here. And so the cone volume would be:\[V_{cone}=\frac{1}{3}\pi(2ft)^2(9.5ft-8ft)\]Adding those together, we would get:\[V_{silo}=V_{cylinder}+V_{cone}=\pi(2ft)^2(8ft)+\frac{1}{3}\pi(2ft)^2(9.5ft-8ft)\]

Answer 16

Actually, that would make your answer A.

Answer 17

thank you

Answer 18

:-) No problem!