Question

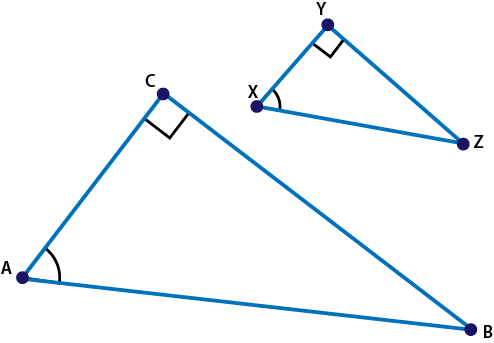
Triangle XYZ was dilated by a scale factor of 2 to create triangle ACB and tan ∠X = 5 over 2 and 5 tenths.




Triangles XYZ and ACB; angles Y and C both measure 90 degrees, angles A and X are congruent.


Part A: Use complete sentences to explain the special relationship between the trigonometric ratios of triangles XYZ and ACB. You must show all work and calculations to receive full credit.

Part B: Explain how to find the measures of segments AC and CB. You must show all work and calculations to receive full credit.
picture below

Answer 1

Let's first find the side lengths for triangle XYZ

assuming you know that tan is opposite over adjacent, we know that
YZ = 5
XY=2.5

Answer 2

And because triangle XYZ was dilated with a scale factor of 2, to create the other triangle, we know for sure that these two triangles are similar, and the angles are equal too
angle C equals angle Y
angle A equals angle X
angle B equals angle Z

Answer 3

And the special relationship is, that they are all equal, because with a scale factor of two, all the trig ratios in triangle ABC will simplify to the trig ratios of triangle XYZ

Answer 4

Not sure when it says "You must show all work and calculations to receive full credit." does it want you to write all the trig ratios out-?
You could write the tan values of each angle, adn compare them with the other triangle, remembering that tan(theta) = opposite/adjacent

Answer 5

For Part B, just write taht because triangle XYZ was dilated with a scale factor of 2 to create triangle ABC, just multiply the sides by 2 to get the sides AC and CB
AC = 2 times XY
CB = 2 times YZ

Answer 6

and so from that, you should know how long AC and BC are

Answer 7

yw