Question

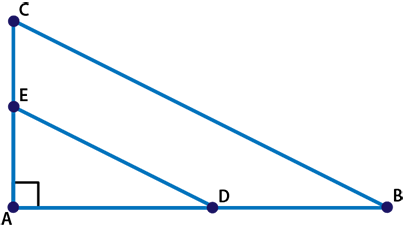
Which statement is not used to prove that ΔABC is similar to ΔADE?

triangles ABC and ADE in which point E is between points A and C on segment AC and point D is between points A and B on segment AB, angle A is a right angle

AC is a transversal line passing ED and CB.
Angle A is congruent to itself, due to the reflexive property.
Segments ED and CB are parallel.
The sum of angles A and B are supplementary to angle C.

Answer 1

Ba dum

Answer 2

Anyone here?

Answer 3

rlly b makin me feel like am retaking mah midterms, mah brain ish fried
anyways tho so time to do process of elimination

Answer 4

Start by doing the process of elimination...

which one of the options prove that ΔABC is similar to ΔADE

Start with A, is AC a transversal line?

Answer 5

I think so

Answer 6

Wait

Answer 7

Alright never mind I think it should be

Answer 8

Since they both pass through two lines right?

Answer 9

Correct. Remember,a transversal is `a line that intersects two other lines.`

Answer 10

Next B, is angle A congruent to its self?

Answer 11

No, i don't think A is congruent
to itself

Answer 12

how so?

Answer 13

Well It doesn't look identical

Answer 14

what do you mean by that? it stayed in the same place?

Answer 15

Oh, so then it would be congruent

Answer 16

Correct, if its congruent, then it can prove ΔABC is similar to ΔADE

and so choice B is eliminated

Answer 17

out of the two choices left, which one does not prove similarity?

Answer 18

I think the answer might be C

Answer 19

are the two segments parallel ?

Answer 20

They seem to be

Answer 21

then C would be eliminated, which leaves us with...?

Answer 22

Oh, so then the answer would be d

Answer 23

correct

Answer 24

Thank you

Answer 25

you're welcome!! :D