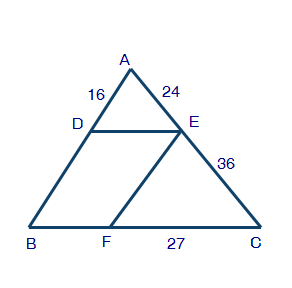
In the figure below, segment DE is parallel to segment BC and segment EF is parallel to AB:

The figure shows triangle ABC with segments DE and DF. Point D is on side AB, point E is on side AC, and point F is on side BC. Segment AD is 16, segment AE is 24, segment EC is 36, and segment FC is 27.
Which statement can be proved true using the given theorem?

Segment BD = 32
Segment BD = 36
Segment BF = 15
Segment BF = 18

Question

In the figure below, segment DE is parallel to segment BC and segment EF is parallel to AB:

The figure shows triangle ABC with segments DE and DF. Point D is on side AB, point E is on side AC, and point F is on side BC. Segment AD is 16, segment AE is 24, segment EC is 36, and segment FC is 27.
Which statement can be proved true using the given theorem?

Segment BD = 32
 Segment BD = 36
 Segment BF = 15
 Segment BF = 18

AsleepAndUnafraid21 · Answer

here is the image

AsleepAndUnafraid21 · Answer

pls help

Extrinix · Answer

Sorry for such a late response @asleepandunafraid21 .

We need to find the scale first off, and to do this we take $\sf{\overline{AE}}$ and put in over $\sf{\overline{EC}}$ $\sf{\dfrac{24}{36}} = 0.7$ Now that we have the scale, we can find the side of $\sf{\overline{DE}}$, which will then allow us to find the approximate length of $\sf{\overline{BF}}$. $\sf{27 \times 0.7 = ?}$ The answer to this should give you roughly the size of the side. Now, it says that you have a given theorem, so this could be an invalid response depending on what that theorem is; but, given the work I’ve done this is the only way I saw to get your answer.

AsleepAndUnafraid21 · Answer

The theorem was: A line parallel to one side of a triangle divides the other two proportionately.

AsleepAndUnafraid21 · Answer

Also, your equation would equal 18.9 which is kinda close to 18

AsleepAndUnafraid21 · Answer

@extrinix plz respond

Extrinix · Answer

@asleepandunafraid21 wrote:

Also, your equation would equal 18.9 which is kinda close to 18

Which would make which statement true? (According to my work)

AsleepAndUnafraid21 · Answer

BF

AsleepAndUnafraid21 · Answer

The third statement

AsleepAndUnafraid21 · Answer

But I was giving you the theorem to see if you still got the same thing

AsleepAndUnafraid21 · Answer

@vocaloid need help for someone to notice and answer question

1 attachment