Question

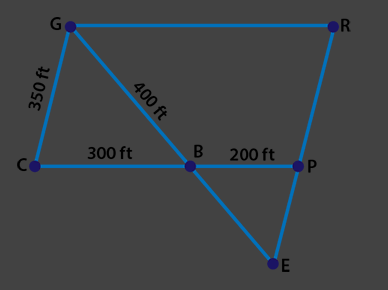
The diagram below models the layout at a carnival where G, R, P, C, B, and E are various locations on the grounds. GRPC is a parallelogram.

Part A: Identify a pair of similar triangles.

Part B: Explain how you know the triangles from Part A are similar.

Part C: Find the distance from B to E and from P to E. Show your work

Answer 1

\[\Delta BGC ~and \Delta ~BEP~are~similar.\]
B.
\[\angle GBC = \angle EBP (vertically~opposite~angles)\]
\[\angle~GCB=\angle~EPB(alternate~angles)\]
\[\angle~CGB=\angle PEB(alternate~angles)\]
so triangles are similar (AAA=AAA)
C.
\[\frac{ CB }{ PB }=\frac{ GB }{ EB }=\frac{ CG }{ PE}\]
\[\frac{ 300 }{ 200 }=\frac{ 400 }{ EB }=\frac{ 350 }{ PE }\]
300EB=400*200
EB=800/3
300PE=350*200
PE=700/3