Question

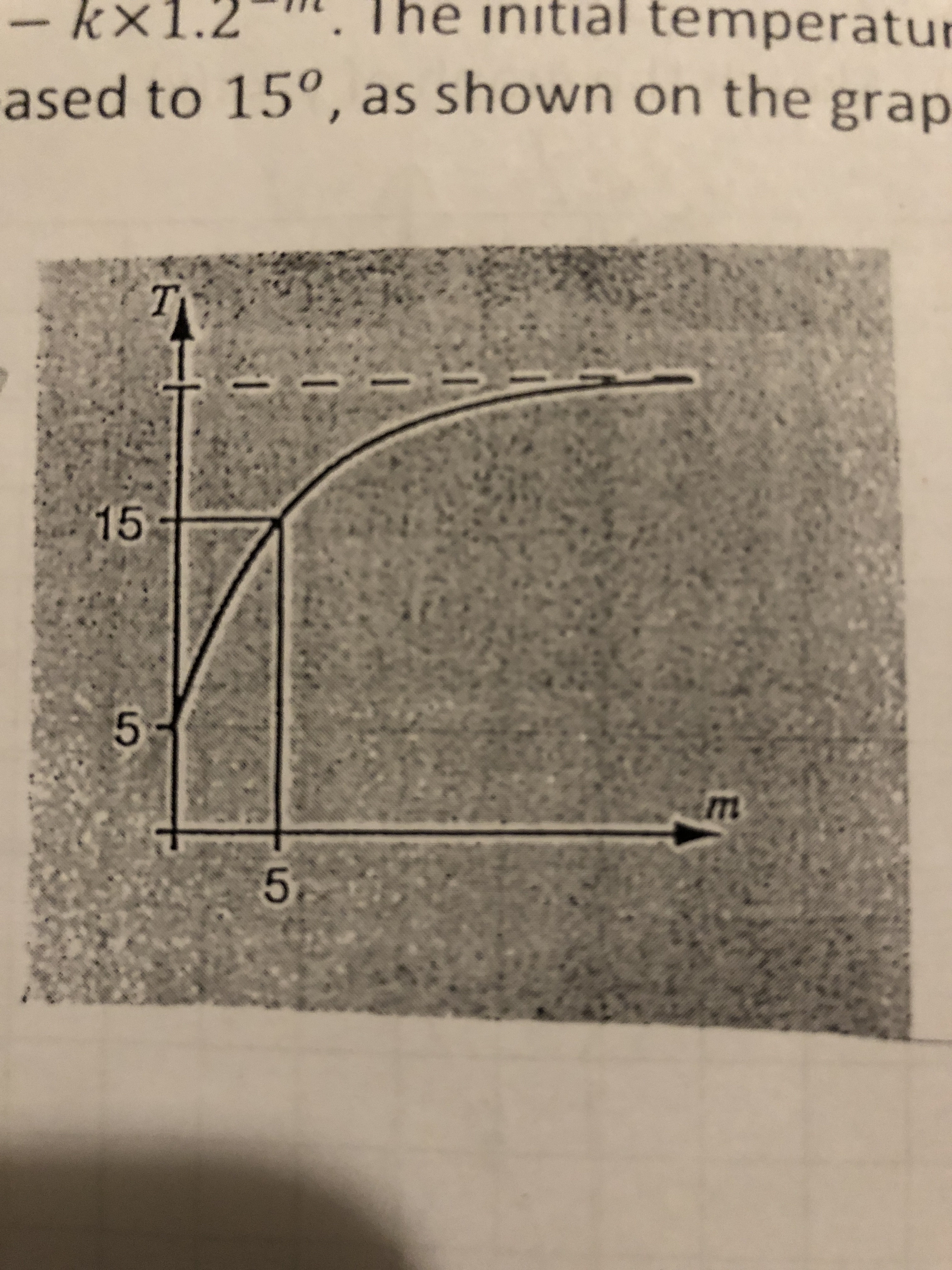
Butter is taken out of the fridge and left to warm up. The temperature of the butter, T (in Celsius degrees), after m minutes is given by the equation T=c-k*1.2^{-m}. The initial temperature of the butter is 5º, and after 5 minutes its temperature has increased to 15º, as shown on the graph
a) Find the values of k and c

Answer 1

Yeaa...nope.

@Vocaloid

Answer 2

\(T(m) = c- k \cdot 1.2^{-m}\)

\( T(0) = 5 \implies c = k + 5\)

\(T(5) = 15 \implies c - k ~ 1.2^{-5} = 5 \)

solve from there

Answer 3

\(T(5) = c - k ~1.2^{-15} = 15\)

Answer 4

oh balls :( you get the picture. just plug in the numbers and solve :)

Answer 5

For T(5), I got
\[c=15+\frac{1}{2.48832}k\]

Answer 6

So then I would do
\[k+5=15+\frac{1}{2.48832}k?\]

Answer 7

the key is to write both equations and solve by elimination

5 = c - k(1.2)^(0)
15 = c - k(1.2)^(-5)

you can subtract these two equations to eliminate c

10 = c - k(1.2)^(-5) - [c - k(1.2)^(0)]

after you eliminate c you should be able to solve for k, then back-substitute to get c

Answer 8

ok I got it now

10 = c - k(1.2)^(-5) - [c - k(1.2)^(0)]

10 = -k(1.2)^(-5) + k

k is about 16.719, then you can select one of the initial points, plug in and solve for c

Answer 9

\[ 5=c-16.719*1.2^{-0}\\
c=21.719\]

Answer 10

good

just to be on the safe side I would double-check those k and c values by plugging them back into the points to see if you still get 5 and 15 ;;

Answer 11

\[ 5=21.719-16.719*1.2^{0}\\
5=5\]

Answer 12

Thank you Vocaloid :P

Answer 13

So: here, Completing the Square is a real timesaver.

Not too shabby  😀

Answer 14

What does the writer imply in this line from the excerpt?

The house, dooryard, barng woodshed was now all full, and when ANOTHER crowd Ritz Cracker I told

Answer 15

What are the coordinates of the point (u22121, 6) after a reflection across the x-axis?

A.

Answer 16

If Oliver Queen takes Slade Wilson to court to sue him for damages and heartache he has caused this would be an example of ___________________ purpose of go

Answer 17

What was NOT true about the economy at the end of World War II?

Answer 18

What was the most commonly held belief of the Social Gospel movement?

Answer 19

I don't see a subject for this.
I just need help not an answer

Assignment Introduction
You are the lead engineer on a project to determine the most-needed

Answer 20

PLEASE HELP
The direction that a wave oscillates is its _________.
A. amplitude
B.

Answer 21

Which of the following is most likely to be an observation made by an anatomist?

RNA polymerase binds to a promoter, a DNA sequence that becomes a gene.

Answer 22

Which statement best describes the nature of science?

Science discoveries using the latest technology are the most valuable.

Answer 23

James Oglethorpe, the founder of Georgia, established good relations with local A

Answer 24

A leather-bound book is completely opaque. Which of the following statements could be true about the book?
A.

Answer 25

Create a paraphrase of the following sentence from u201cThe Cold Equations:u201d
There could be no alternativeu2014but it required a few moments of conditio

Answer 26

Explain how the diction and characterization indicate the authoru2019s purpose for writing about a human rights issue.

Answer 27

Why doesn't glue stick to the inside of the bottle?

Answer 28

Suppose a group of bobcats that normally live and hunt in the tops of mountains, start hunting prey at the base of the mountain and move into the valley bel

Answer 29

Which of these descriptions best characterizes Eisenhower's leadership qualities

Answer 30

When water in a sealed bottle evaporates, the entropy of the water _________.
A. increases
B. decreases
C. remains the same

Answer 31

Wren recorded an outside temperature of u20132u00b0F at 8 a.m. When she checked the temperature again, it was 4u00b0F at 12:00 p.

Answer 32

Question 27 Unsaved
The supply function for manufacturing a certain item is p(x)=x2+46xu221266.

Answer 33

Elementary particles, such as protons, can be accelerated to relativistic speeds in particle accelerators.