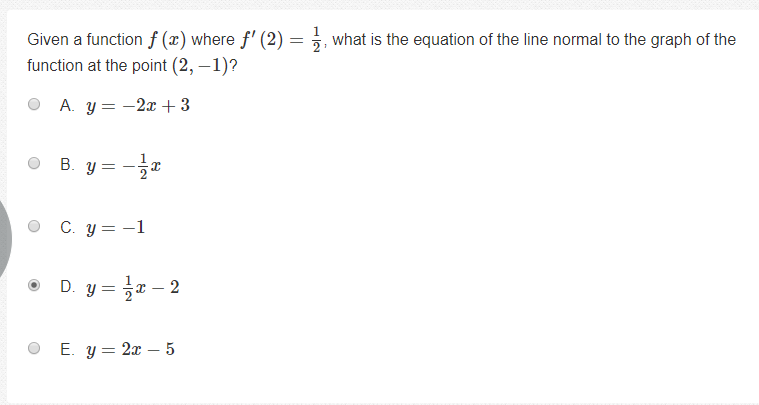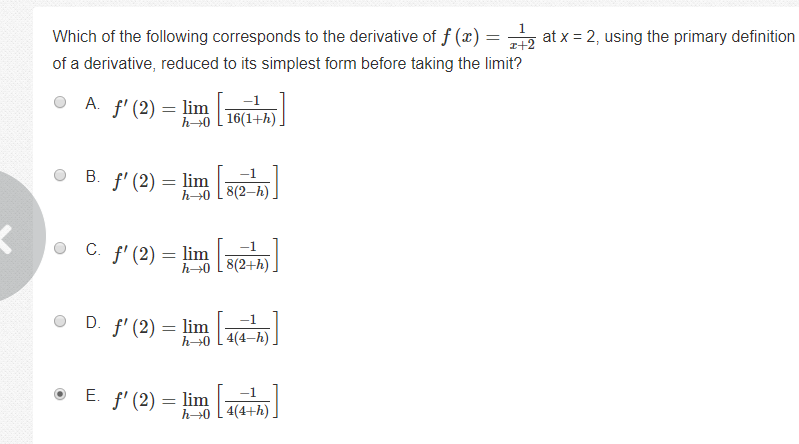Question

need calc checked and finished

Answer 1

@Vocaloid

Answer 2

So, since the derivative of the function f(x) has a value of 1/2 when x=2, we know that f(x) has a slope of 1/2 when x=2. The line Normal to f(x) would be perpendicular to f(x). The slope of the perpendicular line must have be the negative reciprocal of the original line. And the negative reciprocal of 1/2 is -2. So, our answer must have a slope of -2. The only choice with a slope of -2 is A, so our answer should be A.

Answer 3

ty @Vocaloid do you agree?

Answer 4

yeah

Answer 5

can you help with more?

Answer 6

uh

as far as I know the symmetric difference quotient is

[ f(a+h) - f(a-h) ] / 2

where a is the x-value being evaluated, and h is 0.5 as given in the problem

Answer 7

so [ f(2+0.5) - f(2-0.5) ] / 2

disclaimer: I'm not entirely familiar with this concept but that's what I got from the internet.

Answer 8

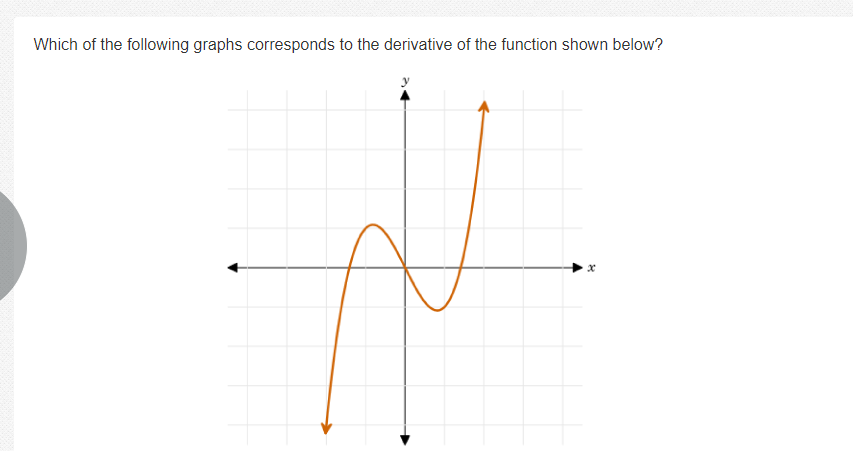
I think the graph of the derivative should look something like this.
At first, the original is increasing, so the derivative should start at a positive value. As the original function approaches -1, the slope decreases to 0, then decreases further to about -1. From there, the slope increases to its original value once again as the graph begins ascending

Answer 9

Hm, I honestly don't know anything about that one, sorry

Answer 10

@photonics

Answer 11

Hm, I honestly don't know anything about that one, sorry