Question

precalc

Answer 1

for this problem i am using the angular formulas and found out that it is in position 288 degrees from standard position but it isn't in standard position so I don't know how to solve it

Answer 2

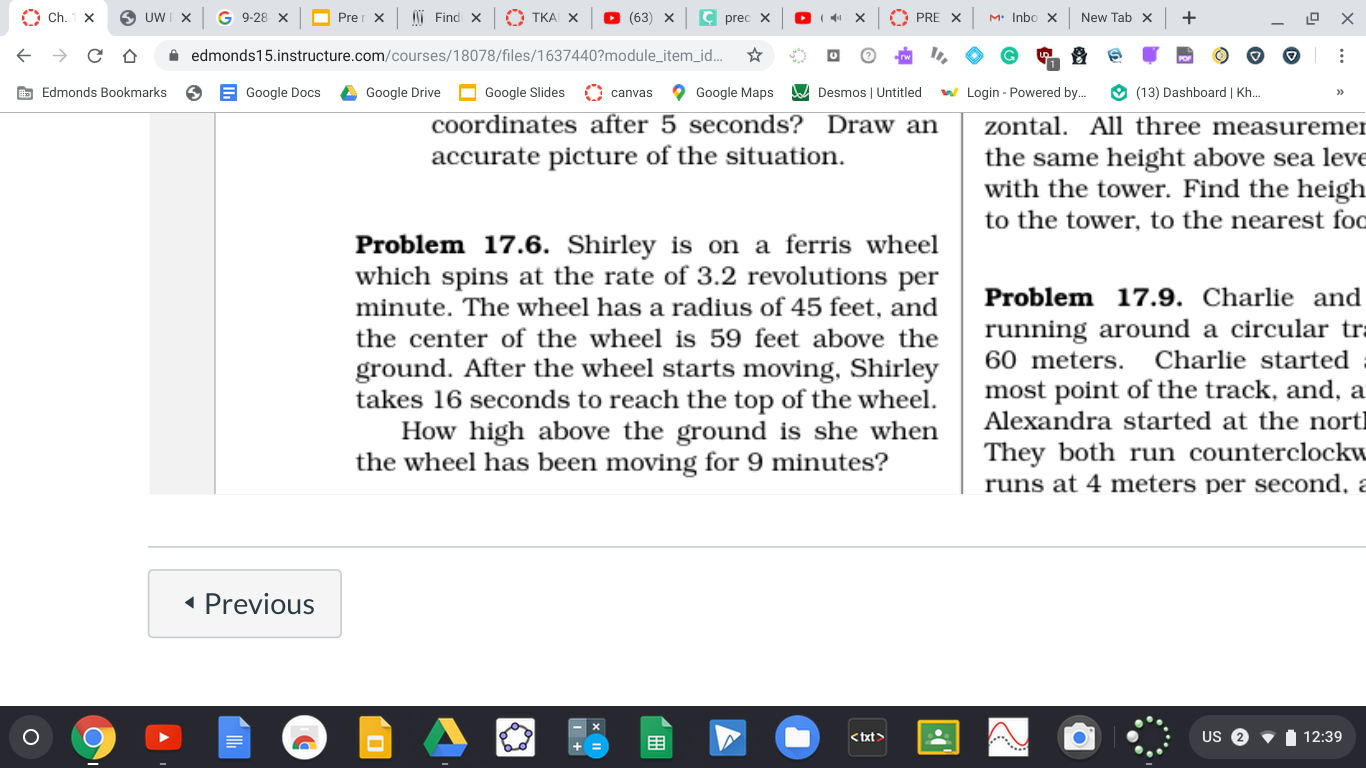
This mimics sinusoidal behavior, hence you'd need to use the function
\(y(t)=rsin(\omega t - \phi )+y_o\)

>Since \(r=45 \text{ft}\), then the amplitude would be 45 as well. Hence r=45
>The angular velocity \(\omega\) is 3.2 revolutions / minute. That can be converted to \(3.2\ \frac{rev}{\min}\cdot\frac{1\ \min}{60\ \sec}\cdot\frac{360°}{1\ rev}=\frac{19.2°}{\sec}\) Therefore \(\omega = 19.2°/s\)
>The center is 59 ft up, so \(y_o\) is 59
>The radius of the wheel is 45 ft, and the center is 59 feet above ground. Hence the ferris wheel is 14 feet heigh, and the top of the wheel is at 108 feet. Now you can solve for \(\phi\)
\(108=45sin(19.2(16)-\phi)+59\)
\(\phi=217.2\)

\(∴ y(t)=45sin(19.2t-217.2)+59\)
Now you can convert 9 minutes to seconds (540 seconds) and find y(540)