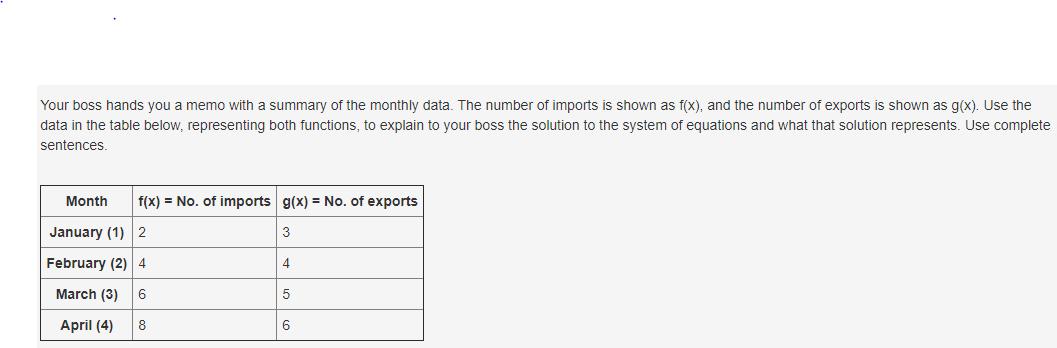
Your boss hands you a memo with a summary of the monthly data. The number of imports is shown as f(x), and the number of exports is shown as g(x). Use the data in the table below, representing both functions, to explain to your boss the solution to the system of equations and what that solution represents. Use complete sentences.

Month f(x) = No. of imports g(x) = No. of exports
January (1) 2 3
February (2) 4 4
March (3) 6 5
April (4) 8 6

Question

Your boss hands you a memo with a summary of the monthly data. The number of imports is shown as f(x), and the number of exports is shown as g(x). Use the data in the table below, representing both functions, to explain to your boss the solution to the system of equations and what that solution represents. Use complete sentences.

Month f(x) = No. of imports g(x) = No. of exports
January (1) 2 3
February (2) 4 4
March (3) 6 5
April (4) 8 6

Hero · Answer

Provide a screenshot of the question from the book

trentV1 · Answer

attachment

Hero · Answer

Okay, so you just have to figure out the equations for $f(x)$ and $g(x)$

trentV1 · Answer

ok

Hero · Answer

Any ideas on how to figure them out?

trentV1 · Answer

Not really im not to good at algebra

Hero · Answer

Okay so the numbers under month are the x values correct?

trentV1 · Answer

Ok

Hero · Answer

We have to figure out the relationship between $x$ and $f(x)$

Hero · Answer

And the relationship between $x$ and $g(x)$

Hero · Answer

So first $x$ and $f(x)$

Hero · Answer

$\displaystyle \begin{array}{|c|c|}
\hline
x & f( x)\
\hline
1 & 2\
\hline
2 & 4\
\hline
3 & 6\
\hline
4 & 8\
\hline
\end{array}$

Hero · Answer

Notice that when $x$ is $1$, $f(x)$ is $2$
When $x$ is $2$ , $f(x)$ is 4, and so on. Do you see a pattern there?

trentV1 · Answer

yea its going up by 2

Hero · Answer

Actually, the correct thought to use in this case is $f(x)$ DOUBLES the value of $x$

Hero · Answer

Or rather $f(x)$ is DOUBLE the value of $x$

Hero · Answer

How could we write the expression for $f(x)$ algebraically knowing this?

trentV1 · Answer

This part im kinda bad at but f(x)=1*2 idk

Hero · Answer

Basically, from the table you observed that $f(x)$ is TWICE the value of $x$. How can we write the expression for $x$ knowing this? Hint: The expression must be written in terms of $x$.

trentV1 · Answer

ig f(2)=x

Hero · Answer

$f(x) = 2x$ actually

Hero · Answer

Try finding the equation for $g(x)$ now.

trentV1 · Answer

g(x)=1x

Hero · Answer

What is the relationship between $x$ and $g(x)$ ?

trentV1 · Answer

+1

Hero · Answer

Yes $g(x)$ increases $x$ by one.

Hero · Answer

So what is the expression for $g(x)$. Try writing it in terms of $x$

trentV1 · Answer

g(x)=1x

Hero · Answer

How do you show that $x$ is INCREASED by one?

Hero · Answer

Your function shows that $x$ is MULTIPLIED by $1$ but not INCREASED by one

trentV1 · Answer

g(x)=x^1 or g(x)=x+1

trentV1 · Answer

I think i got this now i had my parents also help but i appreciate the help thank you for teaching me some of this.

Hero · Answer

You're welcome

1 attachment