Question

Can yall solve☠️ ... Find the equation of the tangent at ( 0 , 2) to the circle with equation
(x + 2)2 + (y + 1)2 = 13

Answer 1

To find the equation of the tangent at (0, 2) to this circle, we first need to find the derivative of the circle's equation. We can then use this derivative to find the slope of the tangent at point (0, 2). Finally, we would use the point-slope form of the equation of a line to find the equation of the tangent.

That is all I can help you with as we are prohibited from giving direct answers.

Answer 2

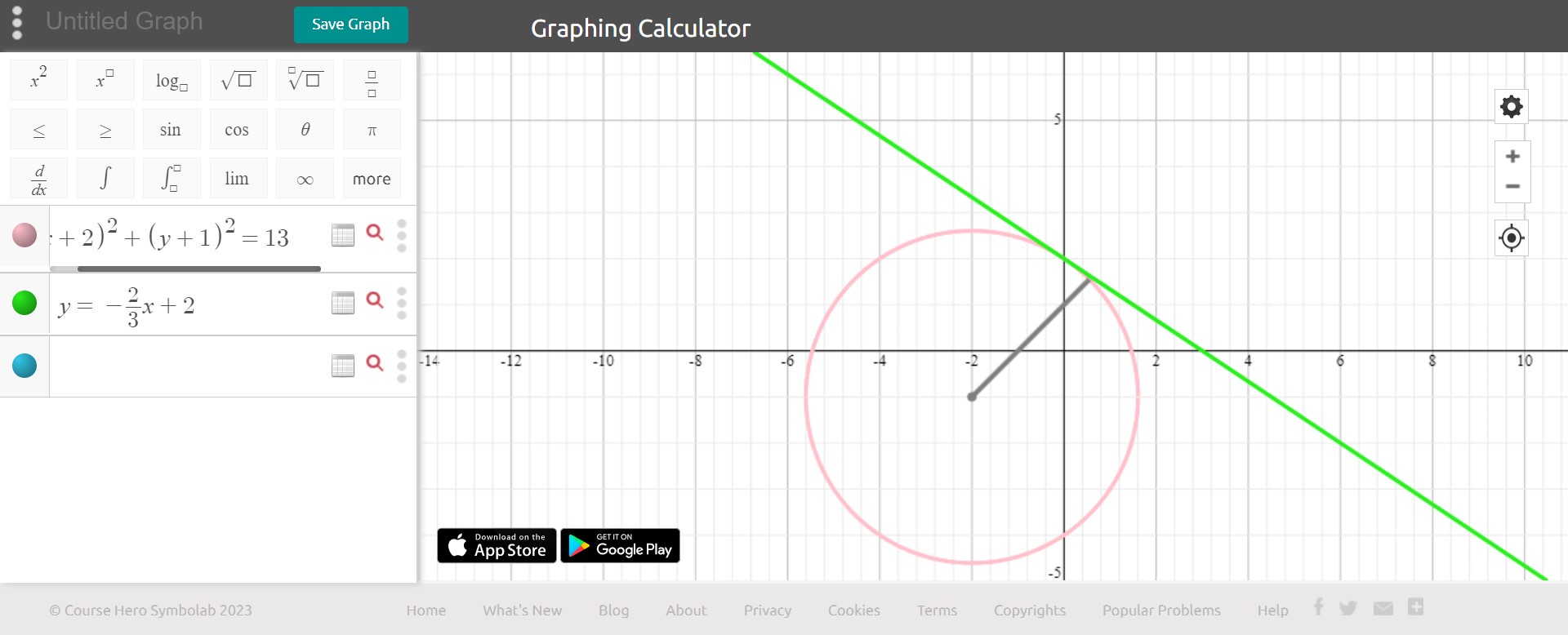
If you want to find it using algebraic methods then you could use:
\[\Large y-b=m(x-a) \]
Where a and b correspond to the points of the tangent line (0,2)
You can find the slope by also using (0,2) and the center of the circle (-2, -1) (using the equation of a circle formula, (h, k) ). Sooo -
\[\large m = \frac{2-(-1)}{0-(-2)}=\frac{3}{2} \]
but since you want the tangent line, you're gonna need to use the negative reciprocal, to get the perpendicular slope: -2/3
Now just plug and chug:
\[\Large y - (2)=-\frac{2}{3} (x-0)\]

Answer 3

And just to be sure, I graphed them:

Answer 4

\[\left( x+2 \right)^2+\left( y+1\right)^2=13\]
or
\[x^2+4x+4+y^2+2y+1=13\]
\[x^2+y^2+4x+2y-8=0\]
compare with \[x^2+y^2+2gx+2fy+c=0\]
eq. of tangent at (x1,y1) is
\[xx1+yy1+g(x+x1)+f(y+y1)+c=0\]
g=2,f=1,c=-8
x1=0,y1=2
eq. of tangent is
x(0)+y(2)+2(x+0)+1(y+2)-12=0
or
2y+2x+y+2-8=0
or
2x+3y-6=0