Question

Slope Tutorial
Creator of Tutorial: iGreen

Answer 1

\(\huge\bf Types~of~Slope:\)

\(\bf\small Positive~Slope:\)

Positive slope rises from LEFT to RIGHT.

\(\bf\small Negative~Slope:\)

Negative slope declines from LEFT to RIGHT.

Examples of Positive and Negative Slopes:



\(\bf\small No~ Slope:\)

Lines with no slope are horizontal, and parallel to the x-axis.

Example:



\(\bf\small Undefined~Slope:\)

Lines with undefined slope are vertical, and parallel to the y-axis.

Example:



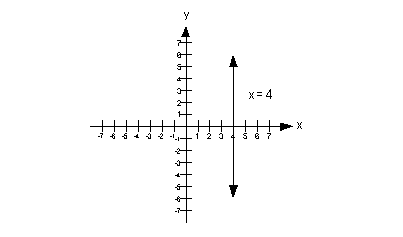\(\huge\bf Finding~Slope:\)

There are 3 different ways to find slope.

\(\bf Equations:\)

Some equations just give you the slope, for example:

\(\bf\small Slope-intercept~form:\)

\(y = \color{lime}mx + \color{blue}b\)

Where \(\color{lime}m\) = slope, and \(\color{blue}b\) = y-intercept.

So if we have:

\(y = \color{lime}2x + \color{blue}5\)

Our slope will be \(\color{lime}2\).

\(\bf\small Point-Slope~form:\)

\(y - \color{blue}{y_1} = \color{lime}{m}(x -\color{yellow}{ x_1})\)

Where \(\color{lime}m\) = slope, \(\color{blue}{y_1}\) = y-value on the line, and \(\color{yellow}{x_1}\) = x-value on the line.

So if we have:

\(y - \color{blue}5 = \color{lime}5(x - \color{red}2)\)

Our slope will be \(\color{lime}5\).

But some equations like:

\(\bf\small Standard~form:\)

\(Ax + By = C\)

To find the slope of the equation, we have to rearrange it into slope-intercept form(\(y = \color{lime}mx + \color{blue}b\)).

So if we have:

\(2x + 3y = 6\)

First, we subtract 2x to both sides:

\(3y = -2x + 6\)

Now we divide 3 to all terms:

\(y = \color{lime}{-\dfrac{2}{3}}x + \color{blue}2\)

Now we can see that the slope of the equation is \(\color{lime}{-\dfrac{2}{3}}\), and the y-intercept is \(\color{blue}2\).

\(\bf Graph:\)

Slope is also defined as: \(\dfrac{Rise}{Run}\). We can see this on graphs of lines.

\(\bf\small Rise:\)

Rise represents the numerator of the slope(ex: In \(m = \dfrac{1}{2}\) 1 is the rise).

Rise can be either going up or down, where up brings a positive number and down brings a negative.

\(\bf\small Run:\)

Run represents the denominator of the slope(ex: In \(m = -\dfrac{4}{5}\) -5 is the run).

Graph example:



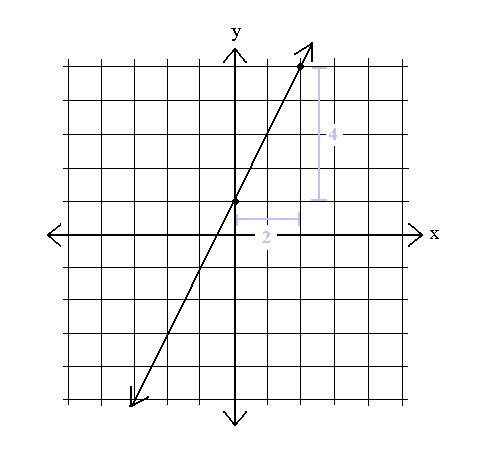We can see that the rise here is \(4\), and the run is \(2\), that means the slope will be \(\dfrac{4}{2}\) which simplifies to \(2\).

\(\bf Formula:\)

The formula for slope is \(m = \dfrac{y_2-y_1}{x_2-x_1}\).

This formula is mostly used to find the slope between two points(ex: (2, 3) and (5, 8)). But it can also be used to find the slope on a graph, where we can just take two points from that graph and plug them in.

If we are given:

\((\color{red}5,\color{lime} 6)\) and \((\color{yellow}8, \color{blue}{12})\)
^ ^ = \(\color{lime}{y_1}\) ^ ^ = \(\color{blue}{y_2}\)
| = \(\color{red}{x_1}\) | = \(\color{yellow}{x_2}\)

Plug them into the slope equation:

\(m = \dfrac{\color{blue}{y_2}-\color{lime}{y_1}}{\color{yellow}{x_2}-\color{red}{x_1}}\)

\(m = \dfrac{\color{blue}{12}-\color{lime}6}{\color{yellow}8-\color{red}5}\)

Subtract the terms in the numerator and the denominator:

\(m = \dfrac{6}{3}\)

Simplify by dividing:

\(m = 2\)

Therefore the slope between \((5, 6)\) and \((8, 12)\) is \(\color{red}2\).

Answer 2

thanks